三角法は、直角三角形の辺の角度と長さの関係を扱う数学の重要な分野です。 6 つの三角比または関数は、サイン、コサイン、タンジェント、コセカント、セカントであり、三角比は直角三角形の辺間の比です。サイン、コサイン、タンジェント関数は 3 つの重要な三角関数です。他の 3 つの関数、つまりコセカント、セカント、コタンジェント関数はそれぞれサイン、コサイン、タンジェント関数の逆関数であるためです。
- sinθ = 対辺/斜辺
- cosθ = 隣辺/斜辺
- Tanθ = 反対側/隣接側
- cosec θ = 斜辺/反対側
- sec θ = 斜辺/隣接辺
- cotθ=隣接面/反対面
タンジェント関数は、次の関数で使用される 6 つの三角関数の 1 つです。 三角関数の公式 。
目次
接線の公式
直角三角形の角度の正接は、指定された角度に対する反対側の長さと隣接する側の長さの比です。正接関数はtanと書きます。直角三角形 XYZ を考えます。その鋭角の 1 つが θ です。反対側とは角度θの反対側であり、隣接側とは角度θに隣接する側である。
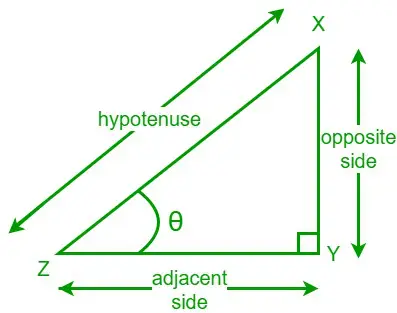
ここで、指定された角度 θ の接線の公式は次のようになります。
Tanθ = 反対側/隣接側
いくつかの基本的な接線公式
象限の正接関数
正接関数は、第 1 象限と第 3 象限では正となり、第 2 象限と第 4 象限では負になります。
- Tan (2π + θ) = Tan θ (1セント四分円)
- Tan (π – θ) = – Tan θ (2nd四分円)
- Tan (π + θ) = Tan θ (3rd四分円)
- Tan (2π – θ) = – Tan θ (4番目四分円)
負の関数としての正接関数
負の角度の正接は正の接線角度の負の値であるため、正接関数は負の関数です。
Tan (-θ) = – Tan θ
サイン関数とコサイン関数に関するタンジェント関数
正弦関数と余弦関数の観点から見た正接関数は次のように記述できます。
Tanθ = sinθ/cosθ
Tan θ = 反対側/隣接側であることがわかります。
次に、分子と分母を斜辺で割ります。
Tanθ = (反対側/斜辺)/(隣接側/斜辺)
sin θ = 反対側/斜辺 であることがわかります。
cos θ = 隣接辺/斜辺
したがって、tanθ = sinθ/cosθ
正弦関数による正接関数
正弦関数の観点から見た正接関数は次のように書くことができます。
Tanθ = sinθ/(√1 – sin 2 私)
私達はことを知っています、
Tanθ = sinθ/cosθ
ラドヤード・キプリングによる一行ごとの説明の場合
ピタゴラス的恒等式から、次のようになります。
それなし2θ+cos2θ = 1
コス2θ = 1 – 罪2私
cosθ = √(1 – sin2私)
したがって、tanθ = sinθ/(√1 – sin2私)
コサイン関数によるタンジェント関数
コサイン関数の観点から見たタンジェント関数は次のように書くことができます。
タンθ = (√1 -cos 2 i)/cos i
私達はことを知っています、
Tanθ = sinθ/cosθ
ピタゴラス的恒等式から、次のようになります。
それなし2θ+cos2θ = 1
それなし2θ = 1 – cos2私
sinθ = √(1 – cos2私)
したがって、tanθ = (√1 – cos2i)/cos i
コタンジェント関数に関するタンジェント関数
コタンジェント関数の観点から見たタンジェント関数は次のように書くことができます。
Tanθ = 1/cotθ
または
Tan θ = cot (90° – θ) (または) cot (π/2 – θ)
コセカント関数によるタンジェント関数
コセカント関数の観点から見たタンジェント関数は次のように記述できます。
Tanθ = 1/√(cosec 2 i – 1)
ピタゴラス的恒等式から、次のようになります。
コセック2θ – コット2θ = 1
ベビーベッド2θ = コ秒2私 – 1
cot θ = √(cosec2i – 1)
私達はことを知っています、
Tanθ = 1/cotθ
したがって、tanθ = 1/√(cosec2i – 1)
正割関数による正接関数
セカント関数の観点から見たタンジェント関数は次のように書くことができます。
タンθ = √秒 2 私 – 1
ピタゴラス的恒等式から、次のようになります。
秒2θ – それで2θ = 1
タンθ = 秒2私 – 1
したがって、tanθ = √(秒2i – 1)
倍角に関する正接関数
倍角の正接関数は、
Tan 2θ = (2 Tan θ)/(1 – Tan 2 私)
三重角による正接関数
三重角の正接関数は、
Tan 3θ = (3 Tanθ – Tan 3 θ) / (1 – 3tan 2 私)
半角による正接関数
半角の正接関数は次のようになります。
Tan (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
Tan (θ/2) = (1 – cos θ) / ( sin θ)
2 つの角度の加算と減算に関するタンジェント関数
正接関数の和と差の公式は次のとおりです。
Tan (A + B) = (tan A + Tan B)/(1 – Tan A Tan B)
Tan (A – Tan B) = (tan A – Tan B)/(1 + Tan A Tan B)
三角比表
| 角度(度単位) | 角度(ラジアン単位) | 私は罪を犯します | cosθ | Tanθ = sinθ/cosθ | コ秒θ | 秒θ | ベビーベッド私 |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | 未定義 | 1 | 未定義 |
| 30° | p/6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 Wordの透かし | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = 未定義 | 1 | 未定義 | 0 |
| 120° | 2人/3人 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(23) | -√3 |
| 180° | 円周率 | 0 | -1 | 0/(-1) = 0 | 未定義 | -1 | 未定義 |
接線公式の解決例
例 1: sin θ = 2/5 で、θ が第 1 象限の角度である場合、tan θ の値を求めます。
解決:
考えると、
- sinθ = 2/5
私たちが持っているピタゴラス的アイデンティティから、
それなし2θ+cos2θ = 1
コス2θ = 1 – 罪2θ = 1 – (2/5)2
コス2θ = 1 – (4/5) = 21/25
cosθ = ±√21/5
θ は第 1 象限の角度であるため、cos θ は正になります。
cosθ = √21/5
私達はことを知っています、
Tanθ = sinθ/cosθ
= (2/5)/(√21/5) = 2/√21
タンθ = 2√21 /21
したがって、sin θ = 2/5 で θ が第 1 象限にあるときの Tan θ の値は (2√21) /(21) となります。
例 2: sec x = 13/12 で x が第 4 象限角度の場合、tan x の値を求めます。
解決:
与えられた秒 x = 13/12
ピタゴラス的恒等式から、次のようになります。
秒2× – それで2x = 1
それで2x = 秒2x – 1= (13/12)2- 1
それで2x = (169/144) – 1= 25/144
Tanx = ± 5/12
Inkscape vs Gimpx は第 4 象限の角度であるため、tan x は負になります。
タン x = – 5/12
したがって、 タン x = – 5/12
例 3: Tan X = 2/3、tan Y = 1/2 の場合、tan (X + Y) の値はいくらですか?
解決:
考えると、
タン X = 2/3 およびタン Y = 1/2
私達はことを知っています、
タン (X + Y) = (タン X + タン Y)/(1 – タン X タン Y)
Tan (X + Y) = [(2/3) + (1/2)]/[1 – (2/3)×(1/2)]
= (7/6)/(2/3) = 7/4
したがって、 Tan(X + Y) = 7/4
例 4: 直角三角形の隣り合う辺が 4 cm、向かい合う辺が 7 cm である場合の正接関数を計算します。
解決:
考えると、
隣接する辺 = 4 cm
反対側 = 7 cm
私達はことを知っています、
Tanθ = 反対側/隣接側
タンθ = 7/4 = 1.75
したがって、 タンθ = 1.75
例 5: 高さ 100 メートルの時計塔を、男性が塔の頂上に対して 60 度の角度で見ています。その男と塔のふもとの間の距離はどれくらいですか?
解決:
考えると、
タワーの高さ = 100 m、θ = 60°
人間と塔のふもとの間の距離 = d とする
我々は持っています、
Tanθ = 反対側/隣接側
タン60° = 100/日
√3 = 100/d [したがって、60° = √3]
d = 100/√3
したがって、人間と塔のふもとの間の距離は 100/√3
例 6: sin θ = 7/25、sec θ = 25/24 の場合の Tan θ の値を求めます。
解決:
考えると、
sinθ = 7/25
秒θ = 25/24
私達はことを知っています、
secθ = 1/cosθ
25/24 = 1/cosθ cosθ = 24/25
我々は持っています、
Tanθ = sinθ/cosθ
= (7/25)/(24/25)
= 7/24
したがって、 タンθ = 7/24
例 7: cosec θ = 5/3、θ が第 1 象限角度の場合の Tan θ の値を求めます。
解決:
与えられた場合、cosec θ = 5/3
ピタゴラス的恒等式から、次のようになります。
10mlからオンスコセック2θ – コット2θ = 1
ベビーベッド2θ = コ秒2私 – 1
コットθ = (5/3)2– 1 = (25/9) – 1 = 16/9
コットθ = ±√16/9 = ± 4/3
θ は第 1 象限の角度であるため、コタンジェント関数とタンジェント関数は両方とも正です。
コットθ = 4/3
私達はことを知っています、
cotθ = 1/tanθ
4/3 = 1/tanθ
タンθ = 3/4
したがって、 タンθ = 3/4
例 8: sin θ = 3/7 で、θ が第 1 象限角度の場合、tan 3θ を求めます。
解決 :
与えられた場合、sin θ = 12/13
私たちが持っているピタゴラス的アイデンティティから、
それなし2θ+cos2θ = 1
コス2θ = 1 – 罪2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cosθ = ±√25/169 = ±5/13
θ は第 1 象限の角度であるため、cos θ は正になります。
cosθ = 5/13
私達はことを知っています、
Tanθ = sinθ/cosθ
= (12/25)/(5/13) = 12/5
したがって、tanθ = 12/5
さて、私たちはそれを知っています、
Tan 3θ = (3 Tan θ – Tan3θ) / (1 – 3 Tan2θ)
Tan 3θ = 3 × (12/5)

