2 つのベクトル間の角度の公式

2 つのベクトル間の角度はそれらの尾部間の角度であり、この角度はベクトル公式の外積と内積を使用して簡単に求めることができます。 2 つのベクトル間の角度は常に 0° ～ 180° の間にあります。

この記事では、2 つのベクトル間の角度、定義、公式、例について詳しく学びます。

2 つのベクトル間の角度とは何ですか?

2 つのベクトル間の角度は、それらの尾部の交点で形成される角度です。 2 つのベクトル間の角度は、ベクトルの方向に応じて、鋭角、直角、または鈍角になります。

2 つのベクトル間の角度は、2 つの公式を使用して求められます。

ベクトルの内積の使用
ベクトルの外積の使用

これは以下の式で説明されます。

2 つのベクトルの間の角度の公式

2 つのベクトル間の角度は、ベクトルのスカラー積を使用して簡単かつ最も一般的に求められます。

2 つのベクトル A と B

内積 A と B の式は次のように与えられます。

vec{A}.vec{B} = |A| |B| cosθ。

特殊なケース

ベクトル間の角度が0度の場合。

つまりθ = 0°です

⇒ |A| |B| cosθ

⇒ |A| |B| cos0°

⇒ |A| |B| [cos0° = 1]

ベクトル間の角度が 180 度の場合。

⇒ |A| |B| cosθ

⇒ |A| |B| cos180°

⇒ – |A| |B| [cos180° = -1]

ベクトル間の角度が90度の場合。

⇒ |A| |B| cosθ

⇒ |A| |B| cos90°

⇒ |A| |B| × 0 [cos90° = 0]

⇒ 0

2 つのベクトル間の角度のコサインは、2 つのベクトルの個々の構成要素の積の合計を 2 つのベクトルの大きさの積で割ったものに等しくなります。

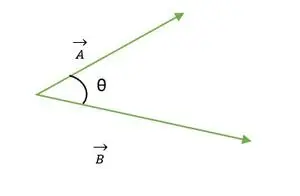
2 つのベクトル A と B

vec{A}.vec{B} =|あ | | B | cosθ。

cosθ=frac{vec{A}.vec{B}}B

θ=cos^-1 frac{vec{A}.vec{B}}B

デカルト形式では、

A = A_バツ私+A_そしてj + A_とk

パワーシェル管理者

B=B_バツi+B_そしてj+B_とk

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

内積の性質

内積は可換です

vec{A}.vec{B}=vec{B}.vec{A}

内積は分配的です

vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})

2 つのベクトル間の角度は 0 ≤ θ ≤ 180 の範囲にあります。両方のベクトルの尾部または頭部が一致すると、ベクトル間の角度が計算されます。

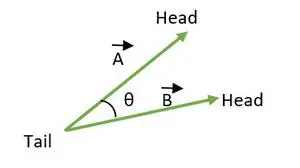
テールの一致

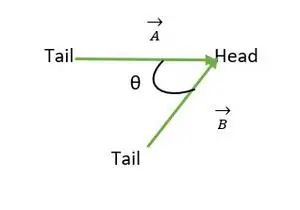
頭の一致

サンプル問題 2 つのベクトル間の角度の公式

問題 1: ベクトル間の角度を求めます (正三角形を形成する場合)

a および b ベクトル
b および c ベクトル
a および c ベクトル

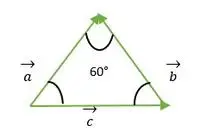
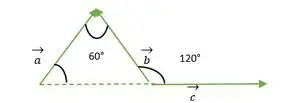
a、b、c ベクトルによって形成される正三角形

解決：

a および b ベクトル
ベクトル a とベクトル b は、両ベクトルの頭が一致するため、ベクトル a とベクトル b の間の角度は、正三角形の 2 辺の間の角度 = 60°と同じになります。

b および c ベクトル:
上の図から、b ベクトルと c ベクトルの先頭または末尾が一致していないことがわかります。

したがって、プロパティを使用することにより、ベクトルはそれ自体と並行して送信された場合、変化しません。

ベクトル c はそれ自体に対して平行にシフトされます

ここで、ベクトル b とベクトル c の尾が互いに一致していることがわかります。したがって、これは正三角形となす外角 = 120° と同じです。

a および c ベクトル

a と c の末尾が一致します
アルゴリズム深さ優先検索

ベクトル a とベクトル c については、両方のベクトルの尾部が一致するため、ベクトル a とベクトル c の間の角度は正三角形の 2 辺の間の角度 = 60°と同じになります。

問題 2: ベクトルが直角二等辺三角形を形成する場合、ベクトル間の角度を求めます。

a と b のベクトル
b と c のベクトル
a および c ベクトル

解決：

a と b のベクトル

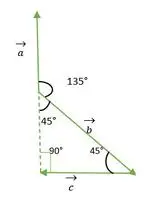
直角二等辺三角形

上の図から、a ベクトルと b ベクトルの先頭または末尾が一致していないことがわかります。したがって、プロパティを使用することにより、ベクトルはそれ自体と並行して送信された場合、変化しません。

ベクトルはそれ自体に対して平行にシフトされます

ここで、a ベクトルと b ベクトルの尾は一致し、直角二等辺三角形の外角と同じ角度 = 135°を作ります。

b と c のベクトル

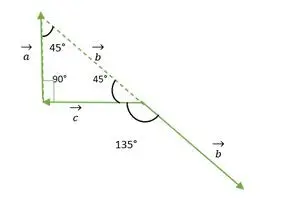
直角二等辺三角形

上図から、b と c のベクトルの先頭または末尾は一致しません。したがって、このプロパティを使用すると、ベクトルがそれ自体と平行に送信された場合、ベクトルは変化しません。

b ベクトルはそれ自体に対して平行にシフトされます

ここで、b ベクトルと c ベクトルの尾部は一致し、直角二等辺三角形の外角と同じ角度 = 135°を作ります。

a および c ベクトル

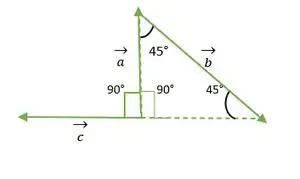
直角二等辺三角形

上の図から、a と c のベクトルの先頭または末尾は一致しません。したがって、プロパティを使用することにより、ベクトルはそれ自体と並行して送信される場合、変化しません。

c ベクトルはそれ自体に対して平行に移動します

ここで、a と c のベクトルの尾部は一致し、角度は二等辺三角形の直角 = 90°と同じになります。

問題 3: ベクトル A = i + j + k とベクトル B = -2i – 2j – 2k の間の角度を求めます。

解決：

式から、

A = A_バツ私+A_そしてj + A_とk

B=B_バツi+B_そしてj+B_とk

cosθ=frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

ここで与えられた質問では、

A= i + j + k

B= -2i -2j -2k

式の値を代入する

⇒ cosθ =frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})}

⇒ cosθ =frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})}

⇒ cosθ =frac{-6}{(sqrt{3}×sqrt{12})}

⇒ cosθ =frac{-6}{(sqrt{36})}

⇒ cosθ = -6/6
すべて置き換える

⇒ cosθ= -1

⇒ θ = 180°

問題 4: ベクトル A = 3i + 4j と B = 2i + j の間の角度を求めます。

解決：

A = A_バツ私+A_そしてj + A_とk

B = B_バツi+B_そしてj+B_とk

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

ここで与えられると、

A= 3i + 4j + 0k

B= 2i + j + 0k

式に値を代入すると、

⇒ cosθ =frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})}

⇒ cosθ =frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})}

⇒ cosθ =frac{(10)}{(sqrt{25}×sqrt{5})}

⇒ cosθ =frac{(10)}{(sqrt{125})}

⇒ θ = cos^-1(frac{(10)}{5.(sqrt{5})})

⇒ θ = cos^-1(frac{2}{(sqrt{5})})

問題 5: ベクトル A = i + j とベクトル B = j + k の間の角度を求めます。

解決：

式から、

A = A_バツ私+A_そしてj + A_とk

B = B_バツi+B_そしてj+B_とk

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

ここで与えられた質問では、

⇒ A = i + j

⇒ B = j + k

⇒ cosθ =frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})}

⇒ cosθ =frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})}

⇒ cosθ =frac{1}{(sqrt{2}×sqrt{2})}

⇒ θ = cos^-1(1/2)

⇒ θ＝60°