の コサイン関数 または コス 関数は簡単に言えば、6 つのうちの 1 つです。 三角関数 三角法の基礎。三角法のコサインは、直角三角形の底辺と斜辺の比として与えられます。コサイン関数は Cos x として表されます。x はコサイン比が計算される角度です。関数の観点から言えば、x はコサイン関数の入力または定義域であると言えます。

一般に、その周期的な性質を利用して、物理学、幾何学、工学などの幅広い主題で広く使用されています。たとえば、音波の波の性質を定義したり、平面を通る電束の計算などに使用されます。この記事では、コサイン関数とは何かについて詳しく学びます。 ドメインと範囲 コサイン関数、周期、コサイン関数のグラフ。

目次

• コサイン関数とは何ですか?
• 単位円内の Cos
• コサイン関数グラフ
• コサイン関数の逆関数
• 微積分のコサイン関数
• Cos関数恒等式

コサイン関数とは何ですか?

コサイン関数は、本質的に基本的に周期的な三角関数です。コサイン関数は cos x として表されます。x は直角三角形の鋭角の 1 つです。コサイン関数は、x の指定された値の底と斜辺の比を求めます。コサイン関数は cos(x) または cos(θ) と省略されます。x はラジアン単位の角度、theta θ はラジアン単位の角度です。 度 一般的に。この記事の後半で説明するように、コサイン関数は単位円、つまり単位半径の円を使用して定義できます。これは本質的に周期的であり、角度が完全に回転するたびにその値を繰り返します。デカルト平面では、x 軸に平行な斜辺のベクトル成分と呼ぶことができます。

コサイン関数の定義

コサイン関数は、直角三角形において、当該角度に隣接する辺の長さと斜辺の長さの比として定義されます。数学的にはコサイン関数は次のように与えられます。

Cos x = Cos θ = 底辺の長さ/斜辺の長さ = b/h = OB/OA

どこ バツ はラジアン単位の角度、θ は度単位の同等の角度です。

Cos関数の領域と範囲

関数の場合、ドメインは許容される入力値であり、範囲はその特定の入力値またはドメイン値の出力値であることがわかっています。したがって、関数は入力を受け取り、それを処理し、特定の出力を与えるプロセッサのように動作すると仮定できます。 cos 関数の定義域と範囲については、以下で説明します。

• コサイン関数の定義域: R つまり、すべての実数のセットです。
• コサイン関数の範囲: [-1, 1]、つまり、出力は -1 から 1 までのすべての実数の間で変化します。

コサイン関数の周期

の 関数 本質的に周期的です。つまり、2π または 360° の後に繰り返されます。言い換えれば、完全に回転するたびにそれが繰り返されます。したがって、コサイン関数の周期は完全な回転、または 360° (または 2π) の角度になります。

コサイン関数の逆数

コサイン関数の逆数は次のように知られています。 割線 機能または 秒 略して。数学的には、コサイン関数の逆数は次のように与えられます。

シェルスクリプトを実行可能にする

sec(θ) = 1/cos(θ)

のルールに従って、 逆数 、Cos x と Sec x を乗算すると、積は常に 1 になります。

コサイン関数グラフ

コサイン関数のグラフはサイン関数のグラフに似ていますが、基本的な違いは、x = 0 の場合、sin 関数のグラフは原点から通過するのに対し、x = 0 の場合、コサイン関数のグラフは y-aixs の (0, 1) から通過することです。以下は、コサイン関数の値、つまり y = cos x のグラフです。

上で説明したプロパティは、関数の周期的な性質と同様にグラフで見ることができます。

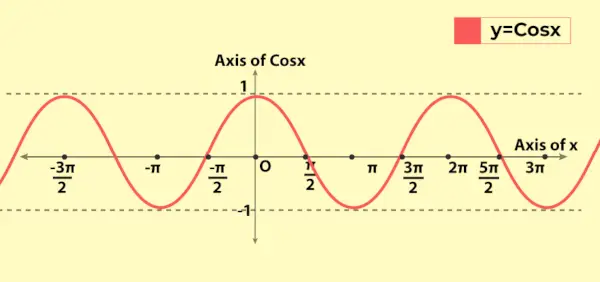
グラフにおけるコサイン関数の変化

コサイン関数の範囲は[-1, 1]なので、グラフでは-1から1まで変化します。グラフが x 軸上の長さ 2π ごとに繰り返されるため、その周期的な性質が示されます。これは、コサイン関数の周期が 2π (または 360°) であることを反映しています。

単位円内の Cos

コサイン関数は単位円を使用して定義できます。単位円に関してコサイン関数を定義する方法を理解しましょう。

点 O を中心に回転する線分 OA を考えます。O はデカルト平面の原点です。したがって、OA の回転は原点 O を中心とする単位円 (単位半径の円) を描き、点 A は常にこの円上に位置します。 A から X 軸に垂線を下ろし、その交点を B とし、OA が X 軸の正の方向となす角度を θ とすると、cos(θ) = x への斜辺の投影となります。 -軸 = OB/|OA| = OB (|OA| = 1 単位のため)。

次の図に示すように、方向 OB が重要であることに注意してください。緑色のセグメントは長さ/大きさを示し、矢印は cos(θ) の方向 (+ve または -ve) を示します。

cos(θ) の値は、第 1 象限と第 4 象限に属する θ では正ですが、第 2 象限と第 3 象限に属する θ では負であることに注意してください。

コサイン関数の逆関数

として知られるコサイン関数の逆関数 逆余弦 関数と略されます アークコス(x) または コス ^-1 （バツ） は次のように定義されます

cos(x) = y

⇒ コス ^-1 (y) = x

逆余弦関数の領域と範囲

逆コサイン関数の定義域と範囲は以下のとおりです。

• 逆コサイン関数の領域: [-1, 1] の範囲内のすべての実数
• 逆余弦関数の範囲: [0, π] の範囲内のすべての実数

双曲線余弦関数

双曲線関数は、代数表現が指数関数の項で行われる三角関数とアナログ的に等価です。双曲線余弦関数は次のように省略されます。 コッシュ(x) どこ バツ 双曲角は双曲幾何学の概念です。同様に、(cos(x), sin(x)) は単位円上の点を表し、(cosh(x), sinh(x)) は単位双曲線上の点を表します。つまり、xy = 1 (sinh(x) は双曲線を表します)正弦関数。双曲線 cos 関数の代数展開は次のように与えられます。

cosh(x) = (e ^バツ +と ^-バツ )/2

双曲線関数の詳細についてはこの記事の範囲を超えていますが、以下を参照してください。 この記事 。

微積分のコサイン関数

数学における微積分の分野では、 差別化と統合 与えられた関数の。関数の微分は、独立変数に対する関数の変化率です。一方、積分は、導関数が存在する関数の積分を求める微分の逆のプロセスです。

コサイン関数の導関数

の 派生関数 コサイン関数の負はサイン関数の負に等しい。数学的に

d(cos(x))/dx = -sin(x)

コサイン関数の積分

の 不定積分 コサイン関数のαはサイン関数と等しくなります。数学的に –

∫cos(x)dx = sin(x) + C、ここで C は積分定数です。

サイン関数とコサイン関数

次のグラフは、サイン関数とコサイン関数の主な違いを表しています。

サイン関数とコサイン関数の違い

次の表は、サイン関数とコサイン関数の違いを示しています。

Cos値テーブル

次の表は、デカルト平面の第 1 象限におけるいくつかの一般的な角度に対するコサイン関数の値を示しています。

15°、75°、195°、-15° などの他の一般的な角度の値は、この後で説明する式 cos (x + y) および cos (x – y) を使用することで、これらの値を使用して簡単に計算できます。記事。

チェック、 三角関数表

Cos関数恒等式

コサイン関数に関連する基本的な三角関数の恒等式を以下に示します。

• それなし²(x) + cos²(x) = 1
• cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
• cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
• cos(-x) = cos(x)
• cos(x) = 1/秒(x)
• cos 2x = cos²× – 罪²x = 1 – 2sin²x = 2cos²x – 1 = (1 – タン²x/1 + タン²バツ）
• cos 3x = 4cos³x – 3cos x

関連記事

• 三角関数の微分
• 逆三角関数
• 逆トリガー導関数

コサイン関数に関する解決例

コサイン関数の概念をより深く理解するのに役立つ解決済みの例をいくつか示します。

例 1: コサイン関数の最大値と最小値はいくらですか?

解決：

コサイン関数の最大値は 0° および 180° で 1 ですが、関数の最小値は 180° で -1 です。

例 2: コサイン関数の値は [0, 360] の範囲内のどの角度で 0 になりますか?

解決：

コサイン関数の値は角度 90° と 270° で 0 になります。

例 3: コサイン関数の値が負になる象限はどれですか?

解決：

II ではコサイン関数が負になります。^ndとⅢ^rd四分円。

例 4: cos (45°) の値を計算します。

解決：

bash 文字列の長さ

上記の恒等式 4 によると、cos(-x) = cos(x) となります。

したがって、cos(-45°) = cos(45°) = 1/√2

例 5: cos(15°) の値を計算します。

解決：

上記の ID 3 を使用する –

cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}

例 6: cos とは何ですか ^-1 (1/2) [0,π] の範囲内?

解決：

コスしてみましょう^-1(1/2) = y。

したがって、上記の範囲では、cos(y) = 1/2 ⇒ y = π/3 となります。

したがって、答えはπ/3となります。

例 7: cos(-15°) の値はいくらですか?

解決：

上記の ID 3 を使用する –

cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} 。

あるいは、恒等式 cos(-x) = cos(x) を使用し、例 5 で計算された cos(15°) の値を使用することもできます。

例 8: x = 0 ～ x = π/2 のコサイン関数のグラフの下の面積を計算します。

解決：

指定された面積は、次の定積分を解くことで計算できます。

int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1

したがって、答えは1単位平方です。

例 9: cos(x) = π/3 の場合、cos(3x) の値を求めます (10 進数 2 桁の精度の 10 進形式)。

解決：

恒等式の使用 – cos(3x) = 4cos³(x) – 3cos(x) –

cos(3x) = 4⨉(π/3)³-3⨉(π/3) ≅ 4.5​​9 – π = 1.45

例 10: cos(120°) の値を求めます。

解決：

cos(2x) の ID の使用

cos(120°) = cos(2⨉60°) = 1 – 2 sin²(60°) = 1- 2⨉(√3/2)²= 1 – 3/2 = -1/2

練習問題: Cos 関数

Q1.直角三角形の角度のcosを計算する公式は何ですか?

Q2.デカルト平面上の cos の幾何学的解釈は何ですか?

Q3. cos(120°)の値を計算します。

Q4. cosの値を求める ^-1 (√3/2) [π, 2π] の範囲。

Q5.ポールが地面に同じ長さの影を落とす場合、太陽が東の方向にある場合、地面に対する太陽の角度を求めます。

要約 - コサイン関数

cos(x) として示されるコサイン関数は、直角三角形の底辺と斜辺の比として定義される基本的な三角関数であり、その周期的な性質により、物理学、工学、幾何学などのさまざまな分野で不可欠です。 、これは波の挙動をモデル化するのに役立ちます。すべての実数の領域と -1 から 1 の範囲を持ち、2 ごとにサイクルを繰り返します。 円周率 ラジアンまたは 360 度。(0,1) から始まる波状のグラフから明らかです。微積分の観点から言えば、cos(x) の導関数は − sin( バツ )、その積分により sin( バツ )+ C 、積分定数として C を使用します。この関数は cosh(x) などの双曲線形式にも拡張され、波動計算や物理システムの振動など、さまざまな数学的コンテキストやソリューションでの応用が強化されています。

コサイン関数: FAQ

1. コサイン関数とは何ですか?

コサイン関数は基本的な三角関数の 1 つです。直角三角形において、当該角度に隣接する辺の長さと斜辺の長さの比として定義されます。

2. 三角関数では Cos と Cos は同じですか?

はい。 cos は、コサイン関数の短縮形です。

3. Cos関数の範囲はどれくらいですか?

cos または cos 関数の範囲は、-1 から 1 までのすべての実数、つまり [-1,1] です。

4. Cos関数の領域とは何ですか?

cos または cos 関数の定義域は、すべての実数の ser です。つまり、 R 。

5. コサイン関数の最大値は何ですか?

コサイン関数の最大値は、0°または 360°に相当するすべての角度に対して 1 です。

6. コサイン関数の最小値は何ですか?

コサイン関数の最小値は、180°に相当するすべての角度で -1 です。

7. Cos(-x) の値を見つけるにはどうすればよいですか?

cos(-x) の値は、cos(-x) = cos(x) の恒等式が存在するため、cos(x) の値を計算することで計算できます。

8. コサイン関数をグラフ化するには?

デカルト平面上にコサイン関数のグラフを描くには、角度をラジアン (または度) で表す x 軸と、x 軸上の対応する角度のコサイン関数の値を表す y 軸を参照します。今、

• ステップ1： グラフを描画したい x 軸のサブセットを取得します。
• ステップ2： この範囲の x 軸を等距離の点に分割します (つまり、すべてのサブポイント間に等しいスペースがあります)。分割数が多いほど、結果として得られるグラフの精度が高くなることに注意してください。
• ステップ 3: これらのサブポイント x のそれぞれについて、グラフ上の点 (x, cos(x)) をマークします。
• ステップ 4: マークされたすべての点を結合して、(選択した x 軸のサブセットの) コサイン関数のグラフを取得します。

9. コサイン関数の周期を見つけるにはどうすればよいですか?

コサイン関数の周期とは、関数が繰り返しを開始するまでの値の最小範囲を指します。コサイン関数は 2π ラジアンを意味する完全な回転ごとに繰り返されることがわかっています。したがって、コサイン関数の周期は 2π ラジアンまたは 360° になります。

10. コサイン関数の振幅とは何ですか?

コサイン関数の振幅は、平均位置、つまり x 軸からの関数の値の最大変位を指します。最大変位が 1 であるため、コサイン関数の振幅は 1 になります (180 度および 0 度の値がそれぞれ -1 および 1 の場合)。コサイン関数の範囲は [-振幅, 振幅] であることに注意してください。