あ 関数 数学における は、入力値のセットと出力値のセットの間の特別な関係です。 Function では、各入力値が特定の出力値を与えます。数学では関数を y = f(x) として表します。 バツ は入力値であり、それぞれ バツ 出力値を y として取得します。

この記事では、次のことについて学びます。 数学における関数とそのさまざまな種類、例などを詳しく説明します。

目次

• 数学における関数とは何ですか?
• 数学における関数定義
• 機能の例
• 関数の条件
• 数学における関数の表現
• 機能の特定
• 機能の種類
• 代数における関数とは何ですか?
• 関数のドメインと範囲
• 機能構成
• 関数代数
• グラフ上の関数とは何ですか?
• グラフ作成機能
• 共通機能
• 関数の応用
• 機能の例
• 関数とは何かについての練習問題

数学における関数とは何ですか?

数学における関数とは、 関係 ドメイン セットの 2 つの変数が範囲セット内の同じ変数にリンクされないように、指定されたセットの入力値 (ドメイン) と出力値 (範囲) の間を調整します。数学における関数の簡単な例は、R→R で定義される f(x) = 2x です。ここでは、ドメイン内の変数は範囲内の 1 つの変数のみに関連付けられます。

数学の関数にはドメイン、コドメイン、範囲があります。ドメインは x のすべての可能な値のセットであり、関数の範囲は y のすべての出力値のセットです。範囲は関数のコドメインのサブセットです。数学における関数は、一意の出力を持つ関係であり、関係の場合のように、関数内に同じ出力を持つ 2 つの入力値は存在しないとも言えます。

数学における関数定義

関数は、定義された関係を介してセット A の各メンバーをセット B の一意のメンバーに接続する特別な関係またはメソッドです。セット A は関数のドメインと呼ばれ、セット B は関数のコドメインと呼ばれます。数学における集合 A から集合 B への関数は次のように定義されます。

f = ∀ a ∈ A、b ∈ B

すべての関数は関係ですが、すべての関係は関数ではありません。関数とみなされるリレーションの基準は、セット A の各要素がセット B に 1 つの画像しか持たないのに対し、リレーションではセット A の要素がセット B に複数のイメージを持つことができるためです。

数学では、空でない集合 A から空でない集合 B までの関数を次のように定義します。

(a, b) ∈ f の場合、f(a) = b

私たちが電話した場所 b のイメージとして ある 関係の下で定義される f 。

あらゆる要素 「あ」 セットAは独特なイメージがあります' b ' セット B の場合、それは関数です。

機能の例

数学の関数 f は、y = f(x) として定義されます。 バツ は入力値であり、x の各入力値に対して、一意の y 値が得られます。 R→R で定義された数学関数のさまざまな例は次のとおりです。

• y = f(x) = 3x + 4
• y = f(x) = sin x + 3
• y = f(x) = -3x²+3など

関数の条件

空ではない任意の 2 つのセット A および B に対して、関数 f:A→B はそれを示します f は A から B への関数です。ここで、 あ はドメインであり、 B は共同ドメインです。

任意の要素 a ∈ A に対して、(a,b) ∈ f となるような固有の要素 b ∈ B が存在します。 aに関係する固有要素bをf(a)と表記し、aのfと読みます。これは、以下の画像からよりよく理解できます。

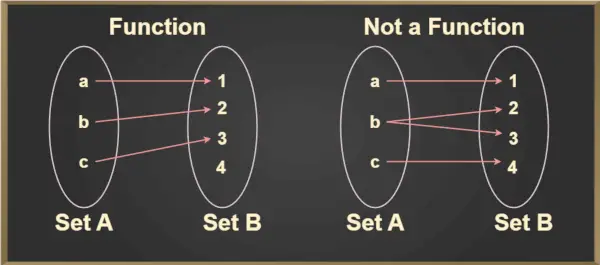
縦線テスト

垂直線テストは、曲線が関数であるかどうかを判断するために使用されます。曲線が複数の点で垂直線を切断する場合、その曲線は関数ではありません。

数学における関数の表現

数学では関数を次のように表します。

y = f(x) = x + 3

ここで、x の値のセットは関数のドメインであり、y の出力値のセットは関数の共ドメインです。ここで、関数は各 x に一意の値を与えるため、すべての実数に対して定義されていますが、x の各値の出力を常に取得できるとは限りません。そのような場合、関数を 2 つの部分に分けて定義します。これは次のように理解できます。

• f(x) = 1/(x – 2)、ここで x ≠ 2
• f(x) = x²ここで、x ∈ {R}

数学における関数は、何らかの入力を受け取り、独自の出力を与える機械として定義できます。関数 f(x) = x²は以下のように定義されます。

数学における関数は次の 3 つの方法で表すことができます。

• 順序付きペアのセット
• テーブルフォーム
• グラフィカルな形式

たとえば、関数を次のように表すと、 f(x) = x³

同じ関数を表す別の方法は次のとおりです。 順序付けされたペアのセット として、

f = {(1,1), (2,8), (3,27)}

上記の集合では、関数の定義域は D = {1, 2, 3}、関数の範囲は R = {1, 8, 27} です。

機能の特定

関数は、数学における特別なタイプの関係として分類されます。関数を識別するために使用できる次のルールがあります。

• 各入力が一意の出力にマッピングされる関係は関数です。これにより、1 対 1 の関数が呼び出されます。
• 2 つの入力 (プリイメージ) が 1 つの出力にマッピングされる関係も関数です。これは多対 1 関数です。
• 1 つの入力が 2 つの異なる出力にマッピングされる関係は関数ではありません。
• 特定の規則に従って多くの入力が多くの出力にマッピングされる関係は関数ではありません。

機能の種類

違う 関数の種類 特に曲線や方程式に関連するさまざまなタイプの数学的問題を解決するために使用されます。数学には、集合 A から集合 B への要素マッピングに基づく 3 つの主要なタイプの関数があります。

単射関数または一対一関数

ドメインの各要素がコドメイン内で異なるイメージを持つ機能は、 単射語 または One to One機能 。

f: f の下で A の異なる要素のイメージが異なる場合、A → B は 1 対 1 または単射的であると言われます。つまり、

f(a ₁ ) = b ₁ 、f(a ₂ ) = b ₂

ここで₁、₂∈ A と b₁、b₂∈ B

全射関数またはオン関数

全射関数は、コドメインのすべての要素がドメイン内に事前イメージを持つ関数です。とも呼ばれます 機能上 これは、コドメインの各要素がドメインの各要素に関連付けられていることを意味します。 codomain の要素は空のリレーションを持つべきではありません。 codomainとrangeの要素数は同じです。

f: A → B は、B のすべての要素が f の下の A のある要素のイメージである場合、つまり、すべての b ϵ B に対して、f(a) となるような A に要素 'a' が存在する場合、オンであると言われます。 = b.

全単射関数

関数が Injective(One to One) と Surjective(Onto function) の両方のプロパティを持つ場合、その関数は と呼ばれます。 全単射関数 。全単射関数では、ドメインの各要素とコドメインの各要素は 1 対 1 の関係にあります。これは、コドメインと範囲の要素の数が同じであり、ドメインまたはコドメインのいずれの要素にも空の関係がないことを意味します。

Pythonでタプルを並べ替える

出力値に基づいて、関数は奇数関数と偶数関数に分類されます。それらを見てみましょう

奇数関数

奇数関数は、原点に対して対称性を示す関数の一種です。具体的には、f(x) が奇関数の場合、f(-x) = -f(x) となります。

偶関数

偶数関数は、y 軸に関して対称性を示す関数の一種です。具体的には、f(x) が偶関数の場合、f(-x) = f(x) が示されます。

代数における関数とは何ですか?

の関数 代数 は、方程式に入れることができる任意の x が方程式から y などの 1 つの出力を生成する方程式です。これは、y = f(x) として表されます。ここで、x は独立変数、y は従属変数です。

例えば：

• y = 2x + 1
• y = 3x – 2
• y = 4y
• y = 5/x

関数のドメインと範囲

ドメインと範囲 関数の は、それぞれ関数の入力値と出力値です。たとえば、f(x) = x として与えられる関数があるとします。²。ここで、すべての実数を x の入力値として受け取ることができ、出力は常に正の実数になります。したがって、その定義域は R で表されるすべての実数のセットであり、その範囲は R で表される正の実数のセットです。⁺

機能構成

f: A → B と g: B→ C が 2 つの関数である場合。 f と g の合成は f(g) として表され、次の関数として定義されます。 フォグ = f(g(x)) (x ∈ A の場合)

2 つの関数 f(x) = x + 3 と g(x) = 2x を考えてみましょう。²

霧 = f(g(x))

⇒ 霧 = f(2x²)

⇒ 歯 = 2倍²+3

もっと詳しく知る、 機能構成

関数代数

関数代数には、2 つの関数間で実行される代数演算が含まれます。 x の実数値に対して定義された 2 つの関数 f(x) と g(x) の代数演算を以下に示します。

• (f + g) (x) = f(x) + g(x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (k f(x)) = k (f(x)); {k は実数であるため}
• (f/g)(x) = f(x) /g(x); {g(x) ≠ 0 の場合}

グラフ上の関数とは何ですか?

関数はグラフ上で簡単に表現できます。グラフ上の関数は、その入力値と対応する出力値にマップされた x-y 平面内の曲線 (直線を含む) を表します。

関数をプロットするには、まず関数上にあるいくつかの点を見つけ、次に関数の軌跡に従ってこれらの点を結合します。たとえば、関数 (直線) f(x) = y = 5x – 2 をグラフ化するには、グラフ上に点が必要です。グラフ上の点を見つけるには、まず x のランダムな値を取得し、次にそれに対応する y の値を次のように見つけます。

f(x) = y = 5x-2

x = 0 の場合、y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

x = 1 の場合、y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

x = 2 の場合、y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

これらの点を結合すると、関数 y = 5x – 2 のグラフが得られます。

グラフ作成機能

x の値がわかれば、関数 f(x) をグラフ上に表現できます。 y = f(x) であるため、x の値から開始して、y に関連する値を見つけることができます。その結果、x 値と y 値を使用して座標平面にグラフをプロットできます。次のシナリオを考えてみましょう。

y = x + 3 と仮定します。

x = 0、y = 3の場合

同様に、

• x = -2、y = -2 + 3 = 1
• x = -1、y = -1 + 3 = 2
• x = 1、y = 1 + 3 = 4
• x = 2、y = 2 + 3 = 5
• x = 3、y = 3 + 3 = 6

結果として、これらの値を使用して関数 x + 3 のグラフをプロットできます。

共通機能

数学で一般的に使用されるいくつかの共通関数については、以下で説明します。

実関数

実関数 数学では、定義域と範囲が実数 (ℝ で示される) の部分集合である関数を指します。より簡単に言うと、実関数とは、各実数入力に実数値を割り当てる数学的規則または関係です。

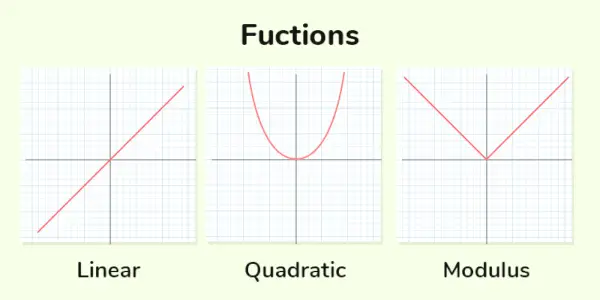
実関数

多項式関数

代数変数の指数が非負の整数である関数は、 多項式関数 。変数のべき乗が 1 の場合は 1 次関数、2 の場合は 2 次関数、3 の場合は 3 次関数と呼ばれます。多項式関数の例をいくつか以下に示します。

• y = x²
• y = 2x + 3
• y = 3x³

多項式関数はさらに次のタイプに分類できます。

一次関数 : 一次関数とは、変数の累乗の最大値が 1 となる関数のことです。 線形関数 は y = mx + c

二次関数 : 二次関数は、変数の最大累乗が 2 となる関数です。 の一般形式 二次関数 は、 斧 ² + bx + c = 0

3次関数 : 3次関数 変数の最大累乗が 3 である関数です。 3 次関数の一般形式は次のように与えられます。 斧 ³ +bx ² + cx + d = 0

逆関数

逆関数 は、別の関数の逆関数を含む関数です。関数 y = f(x) があるとします。その逆関数は x = f になります。^-1(y)。 y = f(x) では、定義域は x で、範囲は y ですが、x = f の場合は、^-1(y)、ドメインは y、範囲は x です。したがって、元の関数の定義域はその逆関数の範囲であり、元の関数の範囲は元の関数の定義域であると言えます。逆関数の例としては、次のようなものがあります。

• y = そう^-1（バツ）
• y = x^-1

エリア機能

面積関数は通常、幾何学的形状または領域の面積を計算する数学関数を指します。 area 関数は 1 つ以上のパラメータを入力として受け取り、対応する形状の面積を返します。エリア機能のいくつかについては以下で説明します。

円関数の面積 : 円の面積 (A) は、次のような半径 (r) の関数です。

A = πr ²

三角関数の面積 : 三角形の面積 (A) は、次のような底辺 (b) と高さ (h) の関数です。

A = (bh)/2

指数関数

指数関数 f(x) = e として表されるものです。^バツ。急速な成長または衰退を示すためによく使用されます。

対数関数

対数関数 は、べき乗の逆演算を表す数学関数です。 f(x) = log x で表されます。

天井機能

天井機能 ⌈x⌉ で示される関数は、実数 x を x 以上の最も近い整数に丸めます。言い換えれば、x 以上の最小の整数値を見つけます。

フロア機能

⌊x⌋ で示される Floor 関数は、実数 x を x 以下の最も近い整数に切り捨てます。言い換えれば、x 以下の最大の整数値を見つけます。

モジュラス関数

モジュラス関数 絶対値関数としても知られ、符号に関係なく実数の大きさまたはサイズを返します。モジュラス関数は ∣x∣ として表されます。ここで、x は入力値です。

シグナム関数

シグナム関数 は、sign 関数またはsignum 関数とも呼ばれ、実数の符号を返す数学関数です。数値が正、負、ゼロのいずれであるかを示します。

三角関数

三角関数 は、直角三角形の角度をその辺の長さに関係付ける数学関数です。 6 つの主要な三角関数は、サイン (sin)、コサイン (cos)、タンジェント (tan)、コセカント (cosec)、セカント (sec)、およびコタンジェント (cot) です。

複雑な関数

入力変数が複素関数である関数はすべて複素関数と呼ばれます。複素数とは、複素平面上にプロットできる数値です。で 複素数 実数と虚数があります。複素数(z)はz= x + iyとして表され、複素関数はf(z) = P(x, y) + iQ(x, y)として表されます。

関数の応用

可変量 y が可変量 x の関数であると言うとき、y は x に依存し、y の値は x の値によって決定されることを示します。この依存関係は、f = y (x) のように表すことができます。

• 円の半径を使用して、円の面積を計算できます。半径 r は領域 A に影響します。関数の数学言語で A が r の関数であると宣言します。 A = f(r) =π×r と書くことができます。²
• 球の体積 V はその半径の関数です。 V = f(r) = 4/3×r³は、r に対する V の依存性を示します。
• 力は、固定質量 m の物体の加速度の関数です。 F = g(a) = m×a。

他の人はこちらも読んでいます:

• 関係と機能
  
• 三角関数の領域と範囲
• 機能の範囲
• 双曲線関数

機能の例

例 1: 2 つの関数の場合、f と g は次のように定義されます。f(x) = x ² そして、g(x) = ln(2x)。合成関数 (gof )( x ) を求めます。

解決：

与えられる:

• f(x) = x²
• g(x) = ln(2x)

(gof )( x ) = g (f (x))

[g (f (x)] = ln(2f(x))

= ln(2x²)

= 2 ln(√2x)

したがって、(gof)(x) = 2 ln(√2x)

例 2: 関数 g(t)= 6t の出力を求める ² +5で

• (i) t = 0
• (ii) t = 2

解決：

与えられた関数、

g(t)= 6t²+5t

• (i) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

例 3: 長方形の長さは幅の 5 倍です。長方形の面積を長さの関数として表します。

解決：

長方形の長さを l、長方形の幅を b とします。

今、

• b = 1/5

長方形の面積(A) = l × l/5 = l²/5

したがって、長方形の面積は、その長さの関数として次のようになります。

A(l) = l ² /5

関数とは何かについての練習問題

1. 関数 f(x)=3x+5 が与えられた場合

• f(2) を見つける
• f(−1) を求めます
• 関数のドメインと範囲を決定します。

2. 関数 g(x)=x が与えられると、 ² – 4x + 3

文字列jsonオブジェクト

• 関数の根を見つけます。
• g(3) と g(0) を求めます。
• 関数の頂点を決定します。

3. 2 つの関数 f(x)=x + 2 および h(x)=2x – 3 が与えられた場合

• 合成関数 (f ∘ h) (x) を求めます。
• (f ∘ h) を評価する(2)

概要 - 関数とは何ですか

数学における関数は、入力値 (ドメイン) と出力値 (範囲) の間の特別な関係であり、各入力は固有の出力に関連付けられます。 y = f(x) として表される関数には特定の特性があり、順序付きペア、表、またはグラフを使用して視覚化できます。これらはさまざまな数学的問題に不可欠であり、単射 (1 対 1)、全射 (onto)、全単射 (両方) などのさまざまなタイプがあります。関数は垂直線テストを使用してテストでき、さらに多項式、逆関数、指数関数、対数関数、三角関数に分類されます。関数を理解するには、そのドメイン、範囲、および関数を定義するルールを認識する必要があります。例には、次のような単純な線形関数が含まれます。 y = 2x + 1 そして複雑な機能の構成。関数は代数、幾何学、微積分学において重要な役割を果たし、数学的関係や現実世界の現象の表現と分析を助けます。

関数とは何かに関するよくある質問

関数の定義とは何ですか?

集合 A で定義された別の集合 B に対する関係 f は、A の各値が集合 B 内で一意の値を持つ場合、数学では関数と呼ばれます。

数学で関数を書くにはどうすればよいですか?

数学における関数 f は f: A → B と表され、次のように定義されます。 f(x) = x + 2。 ここで、x の一意の値ごとに、y の一意の値があります。

関数を変換するにはどうすればよいですか?

関数に対して基本的な代数演算を実行するだけで、関数を他の関数に簡単に変換できます。関数のさまざまな変換には、反射、平行移動、回転などがあります。

有理関数とは何ですか?

分子と分母が多項式関数である分数関数を有理関数といいます。有理関数の例としては、次のようなものがあります。

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1)、 等

一次関数とは何ですか?

関数の各項が定数であるか、1 の累乗を持つ代数関数は、線形関数と呼ばれます。一次関数の例としては、次のようなものがあります。

• f(x) = 2x + 3
• g(x) = x – 5 など

関数のドメインとコドメインとは何ですか?

関数を次のように定義すると、y = f(x) となります。この場合、x の定義域は、y が固有の値となる x のすべての値になります。そして、y の共領域は、x の各値に対する y のすべての値のセットです。

数学で関数をどのように特定しますか?

リレーション内のドメインの入力値 (x) に複数のイメージ (y) がある場合、これらのリレーションは関数になることはできません。したがって、x の値が順序付きペアで繰り返される場合、それは決して関数ではありません。