三角関数テーブル は、0°、30°、45°、60°、90° などの標準角度の三角比の値を見つけるのに役立つ標準テーブルです。それ サイン、コサイン、タンジェント、コセカント、セカント、コタンジェントの 6 つの三角比すべてで構成されます。
三角関数表について詳しく学びましょう。
目次
三角関数テーブル
三角関数表は、共通の角度に対する 6 つの三角関数すべての値を表形式で配置したものです。
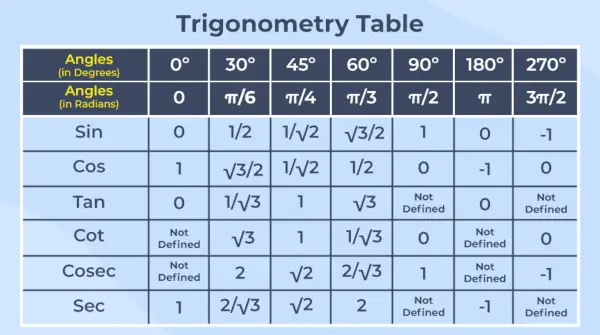
注記 – 三角法は、直角三角形の角度と辺の間の関係を扱う数学の分野です。
三角関数表
三角関数には、サイン、コサイン、タンジェント、コセカント、セカント、コタンジェントという 6 つの基本的な三角関数があります。では、三角関数を見てみましょう。
垂線(P)、底辺(B)、および斜辺(H)を持つ任意の直角三角形の場合、6 つの三角関数は次のとおりです。
| 三角関数の表 | |||
| 関数 | 意味 | 表現 | 直角三角形の辺との関係 |
| 彼の | 垂線と斜辺の比 | それなし 私 | 反対側/斜辺 |
| 余弦 | 底辺と斜辺の比 | コス 私 | 隣辺・斜辺 |
| 正接 | 角度のサインとコサインの比 | それで 私 | 反対側・隣側 |
| コセカント | sinθの逆数 | csc 私 またはコー秒 私 | 斜辺・反対側 |
| 割線 | cosθの逆数 | 秒 私 | 斜辺・隣辺 |
| コタンジェント | Tanθの逆数 | ベビーベッド 私 | 隣接側・反対側 |
注記 – 三角法は、三角形、特に直角三角形の角度と辺の間の関係を扱う数学の分野です。さまざまな分野の問題を解決するために、サイン、コサイン、タンジェント、その他の三角関数の研究と応用が含まれます。
チェック : 三角法: 公式、表、恒等式、比
三角比を学ぶためのトリック
三角比を覚えやすい方法で学習するには、以下の表を参照してください。
| 美しさを演出するために黒髪をカールさせる人もいます |
| sinθ(ある) = 垂線(人) / 斜辺(ある) |
| cosθ(カール) = ベース(黒) / 斜辺(髪) |
| Tanθ(と) = 垂直(生み出す) / 底辺(美しさ) |
三角関数表の覚え方
三角関数の公式をすべて知っていれば、三角関数表を覚えるのは非常に簡単です。という裏技もあります 片手のトリック 三角関数表を暗記します。

ステップ1: 上の図では、正弦テーブルの左側の指の数を標準角度として数えます。
ステップ2: 左側の指の数 (1 番目の手順で計算) を 4 で割ります。
ステップ 3: ステップ 2 で計算した値の平方根を求めます。
チェック: 三角関数の公式 – すべての三角関数の恒等式と公式のリスト
入力信号がありません
トリガーテーブルの作成方法
標準角度の三角関数テーブルを作成するには、次の手順を検討してください。
ステップ 1: テーブルを作成する
テーブルを作成し、次のようなすべての角度をリストします。 0°、30°、45°、60°、90°、 上の行にあります。すべての三角関数 sin、cos、tan、cosec、sec、cot を最初の列に入力します。
ステップ 2: sin 関数のすべての角度の値を評価します。
sin 関数の値を求めるには、0、1、2、3、4 を 4 で割って、それぞれの値の根を次のように計算します。
の値については、 sin 0° = √(0/4) = 0
同様に、
sin 30° = √(1/4) = 1/2
sin 45° = √(2/4) = 1/√2
sin 60° = √(3/4) = √3/2
sin 90° = √(4/4) = 1
| 0°なし | 30°なし | 45°なし | 60°なし | 90°なし |
|---|---|---|---|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1 |
ステップ 3: cos関数のすべての角度の値を評価します。
cos 関数の値は sin 関数の値の逆です。つまり、cos 0° = sin 90°、cos 30° = sin 60°、cos 45° = sin 45°です。
| cos0° | cos30° | cos45° | cos60° | cos90° |
|---|---|---|---|---|
| 1 | √3/2 | 1/√2 | 1/2 | 0 |
ステップ 4: Tan 関数のすべての角度の値を評価する
tan 関数の値は、sin 関数を cos 関数で割ったものに等しくなります。つまり、tan x = sin x / cos x となります。 Tan 関数のすべての角度の値は次のように計算されます。
同様に、tan 0°= sin 0° / cos 0° = 0/1 = 0
| だから0° | それで30° | だから45° | だから60° | だから90° |
|---|---|---|---|---|
| 0 | 1/√3 | 1 | √3 | 定義されていません |
ステップ 5: cosec 関数のすべての角度の値を評価する
cosec 関数の値は、sin 関数の逆数に等しくなります。 cosec 0°の値は、sin 0°の逆数をとることで得られます。
cosec 0° = 1 / sin 0° = 1 / 0 = 定義されていません。同様に、
| コ秒 0° | コセック 30° | コセック 45° | コセック60° | コセック90° |
|---|---|---|---|---|
| 定義されていません | 2 | √2 | 23 | 1 |
ステップ 6: 秒関数のすべての角度の値を評価する
sec 関数の値は cos 関数の逆数に等しくなります。 sec 0°の値は、cos 0°の逆数をとることで得られます。
sec 0° = 1 / cos 0° = 1 / 1 = 1。同様に、
| 秒0° | 秒30° | 秒45° | 秒60° | 秒90° |
|---|---|---|---|---|
| 1 | 23 | √2 | 2 | 定義されていません |
ステップ 7: cot 関数のすべての角度の値を評価する
cot 関数の値は、tan 関数の逆数に等しくなります。 cot 0°の値はtan 0°の逆数をとることで得られます。
cot 0° = 1 /tan 0° = 1 / 0 = 定義されていません。同様に、
| コット 0° | コット 30° | コット 45° | コット60° | コット90° |
|---|---|---|---|---|
| 定義されていません | √3 | 1 | 1/√3 | 0 |
このようにして、次のような三角比の表を作成できます。
| 度およびラジアンの三角関数表 | |||||||
|---|---|---|---|---|---|---|---|
| 角度 (度単位) | 角度 (ラジアン単位) | それなし | コス | それで | コセック | 秒 | ベビーベッド |
| 0° | 0 | 0 | 1 | 0 | 未定義 | 1 | 未定義 |
| 30° | p/6 | 1/2 | √3/2 | 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | √3 | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 未定義 | 1 | 未定義 | 0 |
三角関数の公式
補角と補角に関連するいくつかの三角法の公式について学びましょう。
- 補角: 合計が 90° に等しい角度のペア
- 補助角度: 合計が 180° に等しい角度のペア
チェック: 三角比
補角の三角恒等式
補角の恒等式は、合計が 90 度 (または π/2 ラジアン) になる 2 つの角度の三角関数間の関係に基づいています。これらはとして知られています 共関数恒等式 。
| 三角関数 | 身元 |
|---|---|
| 彼の | sin(90°− 私 )=cos 私 |
| 余弦 | cos(90°− 私 )=なし 私 |
| 正接 | Tan(90°− 私 )=簡易ベッド 私 |
| コタンジェント | コット(90°− 私 )=そう 私 |
| 割線 | 秒(90°− 私 )=csc 私 |
| コセカント | cosec(90°− 私 )=秒 私 |
補助角の三角恒等式
補助角の恒等式は、合計 180 度 (または π ラジアン) になる 2 つの角度の三角関数に関連します。
| 三角関数 | 身元 |
|---|---|
| 彼の | sin(180°− 私 )=なし 私 |
| 余弦 | cos(180°− 私 )=−cos 私 |
| 正接 | タン(180°− 私 )=−タン 私 |
| コタンジェント | コット(180°− 私 )=−コット 私 |
| 割線 | 秒(180°− 私 )=−秒 私 |
| コセカント | cosec(180°− 私 )=cosec 私 |
三角関数恒等表
三角恒等式 は、三角関数の問題を解く際によく使用される恒等式です。さまざまな三角関数の恒等式がありますが、主な三角関数の恒等式は次の 3 つです。
| 三角関数の恒等式の表 | |
| 三角恒等式 | 式 |
| ピタゴラスの恒等式 | それなし2θ+cos2θ = 1 |
| 正割接線恒等式 | 秒2θ – それで2θ = 1 |
| コセカント-コタンジェント恒等式 | コセック2θ – コット2θ = 1 |
また、次のことも確認してください。
- 三角比
- 逆三角恒等式
- 高さと距離
三角関数テーブルの例
三角関数表に関するいくつかの問題を解いてみましょう。
例 1: sin θ = 4/5 の場合、すべての三角関数の値を求めます。
解決:
ここにあります、
iCloud写真にアクセスする方法sinθ = 4/5
as、sin θ = 垂直 / 斜辺
したがって、垂直 (P) = 4 および斜辺 (H) = 5 となります。
つまり、ピタゴラスの定理によれば、 H 2 =P 2 +B 2
塩基(B)の値を調べてみましょう
52=B2+42
25 = B2+16
25 -16 = B2
B2= 9
B = 3今では、
SQL句Sin θ = 垂線/斜辺
= AB/AC = 4/5コサインθ = 底辺/斜辺
= BC/AC = 3/5接線θ = 垂線/底辺
= AB/BC = 4/3コセカント θ = 斜辺/垂線
= AC/AB = 5/4セカント θ = 斜辺/底辺
= AC/BC = 5/3コタンジェント θ = 底辺/垂線
= BC/AB = 3/4
例 2: cos 45° + 2 sin 60° – Tan 60° の値を求めます。
解決:
三角関数表から、
cos 45° = 1/√2、sin 60° = √3/2、tan 60° = √3
したがって、
cos 45° + 2 sin 60° – Tan 60° = 1/√2 + 2(√3/2) – √3
= 1/√2
例 3: cos 75° の値を求めます。
解決:
私達はことを知っています、
cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2cos 75°= (√3 – 1)/2√2。
結論 – 三角関数表
三角関数テーブル は、三角関数のサイン、コサイン、タンジェント、コセカント、セカント、コタンジェントと、さまざまな角度のそれぞれの値に関する包括的なリファレンスを提供します。私 問題を解決するための貴重なツールとして機能します 三角方程式、幾何学的関係の分析、周期現象の動作の理解。 いるかどうか 数学、物理学、工学、またはその他の分野において、三角関数テーブルは計算、問題解決、視覚化に役立ち、三角関数の概念と現実世界のシナリオでのその応用についてのより深い理解に貢献します。
三角関数テーブル – FAQ
三角法とは何ですか?
三角法は、三角形の角度と辺を扱う数学の分野です。
三角関数表とは何ですか?
三角関数テーブルは、一般的な角度に対する 6 つの三角関数すべての値を含むテーブルです。
三角関数表を発明したのは誰ですか?
ギリシャの天文学者 ヒッパルコス (紀元前 127 年) 三角関数表を発明した。
三角関数表の標準角度とは何ですか?
三角関数表の標準角度は0°、30°、45°、60°、90°です。
Tan 45 度の値はいくらですか?
Tan 45 度の値は 1 です。
三角関数表を学ぶにはどうすればよいですか?
三角関数表を覚えるコツは、
- sin 関数のすべての角度のすべての値を学習する必要があります。
- cos 関数のすべての角度の値は、sin 関数の鏡像になります。
- tan 関数の値は、sin 関数を cos 関数で割ることによって計算できます。
- cosec 関数の値は sin の逆数です。
- 同様に、sec と cot は cos と cot 関数の逆数です。
三角関数表の6つの基本関数とは何ですか?
三角関数テーブルの 6 つの基本的な三角関数は、サイン、コサイン、タンジェント、セカント、コタンジェント、コセカントです。
三角関数表に代わる電卓はありますか?
関数電卓は、あらゆる角度の三角比を計算できます8。
三角関数テーブルは何に役立ちますか?
三角関数テーブルは基本的に、すべての角度のすべての三角比の値を見つけるために使用されます。これらの値は、実際の生活に数多く応用されています。
