- 山登りアルゴリズムは、標高/値が増加する方向に継続的に移動して山の頂上や問題に対する最適な解決策を見つけるローカル検索アルゴリズムです。これより高い値を持つ近隣が存在しないピーク値に達すると終了します。
- 山登りアルゴリズムは、数学的問題を最適化するために使用される手法です。山登りアルゴリズムの広く議論されている例の 1 つは、セールスマンの移動距離を最小限に抑える必要がある巡回セールスマン問題です。
- これは、すぐ隣の良好な状態のみを検索し、それ以降は検索しないため、貪欲なローカル検索とも呼ばれます。
- 山登りアルゴリズムのノードには、状態と値の 2 つのコンポーネントがあります。
- ヒルクライミングは、優れたヒューリスティックが利用可能な場合に主に使用されます。
- このアルゴリズムでは、単一の現在の状態のみを保持するため、検索ツリーまたはグラフを維持および処理する必要はありません。
ヒルクライミングの特徴:
以下は、ヒルクライミングアルゴリズムの主な機能の一部です。
ヒルクライミングの状態空間図:
状態空間ランドスケープは、アルゴリズムのさまざまな状態と目的関数/コストの間のグラフを示す山登りアルゴリズムのグラフィック表現です。
Y 軸には目的関数またはコスト関数となる関数が取られ、X 軸には状態空間が取られています。 Y 軸上の関数がコストの場合、検索の目的はグローバル最小値とローカル最小値を見つけることです。 Y 軸の関数が目的関数の場合、検索の目的はグローバル最大値とローカル最大値を見つけることです。
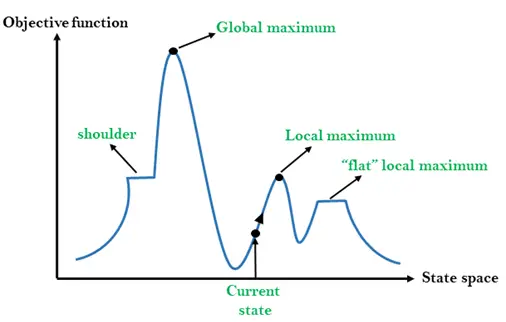
状態空間ランドスケープ内のさまざまな領域:
極大値: 極大値は隣接する状態よりも優れた状態ですが、それよりも高い状態も存在します。
グローバル最大値: 大域的最大値は、状態空間ランドスケープの可能な限り最良の状態です。目的関数の値が最も高くなります。
現在の状態: 現在エージェントが存在するランドスケープ図の状態です。
平坦な極大値: これは、現在の状態に隣接するすべての状態が同じ値を持つ、風景内の平らな空間です。
ショルダー: 上り坂が続く高原地帯です。
山登りアルゴリズムの種類:
- 簡単な山登り:
- 最急登のヒルクライム:
- 確率的山登り:
1. 簡単な山登り:
シンプルヒルクライミングは、ヒルクライミングアルゴリズムを実装する最も簡単な方法です。 一度に隣接ノードの状態のみを評価し、現在のコストを最適化する最初の状態を選択し、それを現在の状態として設定します。 。それが 1 つの後継状態であることのみをチェックし、現在の状態よりも優れていることが判明した場合は、同じ状態になるように移動します。このアルゴリズムには次の特徴があります。
- 時間がかからない
- 最適ではないソリューション、およびソリューションが保証されていない
単純な山登りのアルゴリズム:
- 目標状態の場合は成功を返して終了します。
- それ以外の場合、現在の状態よりも優れている場合は、新しい状態を現在の状態として割り当てます。
- 現在の状態より良くない場合は、ステップ 2 に戻ります。
2. 最も急な登りのヒルクライミング:
最急上昇アルゴリズムは、単純な山登りアルゴリズムのバリエーションです。このアルゴリズムは、現在の状態のすべての隣接ノードを検査し、目標状態に最も近い隣接ノードを 1 つ選択します。このアルゴリズムでは、複数の近傍を検索するため、より多くの時間がかかります。
最急登ヒルクライミングのアルゴリズム:
- SUCC を、現在の状態の後継者がそれより優れているような状態にしましょう。
- 現在の状態に適用される演算子ごとに次のようになります。
- 新しい演算子を適用して、新しい状態を生成します。
- 新しい状態を評価します。
- 目標状態の場合は、それを返して終了します。それ以外の場合は、SUCC と比較します。
- SUCC よりも優れている場合は、新しい状態を SUCC として設定します。
- SUCC が現在の状態よりも優れている場合は、現在の状態を SUCC に設定します。
3. 確率的山登り:
確率的山登りでは、移動する前に隣接するすべてのものを調べません。むしろ、この検索アルゴリズムは、隣接ノードを 1 つランダムに選択し、それを現在の状態として選択するか、別の状態を調べるかを決定します。
山登りアルゴリズムの問題:
1. 極大値: 極大値は、隣接する各状態よりも優れた景観内のピーク状態ですが、極大値よりも高い別の状態も存在します。
解決: バックトラッキング手法は、状態空間ランドスケープにおける極大値の解決策となる可能性があります。アルゴリズムが検索スペースをバックトラックして他のパスも探索できるように、有望なパスのリストを作成します。

2. プラトー: プラトーとは、このアルゴリズムでは最適な移動方向が見つからないため、現在の状態に隣接するすべての状態が同じ値を含む検索空間の平坦な領域です。高原地帯では山登り探索では道に迷ってしまう可能性があります。
解決: プラトーの解決策は、検索中に大きな一歩を踏み出したり、非常に小さな一歩を踏み出して問題を解決することです。現在の状態から遠く離れた状態をランダムに選択するため、アルゴリズムが非プラトー領域を見つける可能性があります。

3. 尾根: リッジは極大値の特殊な形式です。周囲よりも高い面積を持っているが、坂道があり、一度ではたどり着けない。
解決: 双方向検索を使用するか、異なる方向に移動することで、この問題を改善できます。

焼き鈍し法:
山登りアルゴリズムは、極大値に引っかかる可能性があるため、不完全であることが保証され、より低い値に向かって決して移動しません。また、アルゴリズムが後続を移動することによってランダム ウォークを適用する場合、完了する可能性がありますが、効率的ではありません。 焼き鈍し法 は効率と完全性の両方を実現するアルゴリズムです。
機械用語でいうと アニーリング 金属またはガラスを高温で硬化させ、その後徐々に冷却するプロセスです。これにより、金属は低エネルギーの結晶状態に到達します。同じプロセスがシミュレーテッド アニーリングでも使用され、アルゴリズムが最適な手を選択する代わりに、ランダムな手を選択します。ランダムな移動によって状態が改善される場合は、同じ道をたどります。それ以外の場合、アルゴリズムは確率が 1 未満のパスをたどるか、下り坂に移動して別のパスを選択します。
