このチュートリアルは初心者向けのガイドです。 データ構造とアルゴリズムの学習 Pythonを使って。この記事では、リスト、タプル、辞書などの組み込みデータ構造と、次のようないくつかのユーザー定義データ構造について説明します。 リンクされたリスト 、 木 、 グラフ 、など、トラバーサル、およびよく説明された適切な例と練習問題を活用した検索および並べ替えのアルゴリズムを学習します。

リスト

Python リスト 他のプログラミング言語の配列と同様に、順序付けられたデータのコレクションです。リスト内にさまざまなタイプの要素を含めることができます。 Python List の実装は、C++ の Vector や JAVA の ArrayList に似ています。すべての要素を移動する必要があるため、コストのかかる操作は、リストの先頭から要素を挿入または削除することです。事前に割り当てられたメモリがいっぱいになった場合、リストの末尾での挿入と削除もコストがかかる可能性があります。

例: Python リストの作成

List = [1, 2, 3, 'GFG', 2.3] print(List)>

[1, 2, 3, 'GFG', 2.3]>

リスト要素には、割り当てられたインデックスによってアクセスできます。 Python のリストの開始インデックスでは、シーケンスは 0 で、終了インデックスは (要素が N 個ある場合) N-1 です。

例: Python のリスト操作

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3])>

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks>

タプル

Python タプル はリストに似ていますが、タプルは 不変 つまり、一度作成すると変更することはできません。リストと同様に、タプルにもさまざまなタイプの要素を含めることができます。

Python では、データ シーケンスのグループ化に括弧を使用するかどうかにかかわらず、一連の値を「カンマ」で区切って配置することによってタプルが作成されます。

注記： 1 つの要素のタプルを作成するには、末尾にカンマが必要です。たとえば、(8,) は要素として 8 を含むタプルを作成します。

例: Python タプル操作

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3])>

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4>

セット

パイソンセット は、重複を許可しない変更可能なデータのコレクションです。セットは基本的に、メンバーシップのテストと重複エントリの排除を含めるために使用されます。ここで使用されるデータ構造はハッシュです。これは、平均 O(1) で挿入、削除、および走査を実行する一般的な手法です。

同じインデックス位置に複数の値が存在する場合、値はそのインデックス位置に追加され、リンクされたリストが形成されます。 CPython では、ダミー変数を含むディクショナリを使用して実装されます。ここで、キーは、時​​間計算量を大幅に最適化したメンバー セットです。

セットの実装:

単一の HashTable に対する多数の操作を含むセット:

例: Python の集合演算

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set)>

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True>

冷凍セット

冷凍セット Python の は、適用先の固定セットに影響を与えずに結果を生成するメソッドと演算子のみをサポートする不変オブジェクトです。セットの要素はいつでも変更できますが、フリーズされたセットの要素は作成後も同じままです。

例: Python の凍結セット

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h')>

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'})>

弦

Python 文字列 Unicode 文字を表す不変のバイト配列です。 Python には文字データ型はなく、単一の文字は単に長さ 1 の文字列です。

注記： 文字列は不変であるため、文字列を変更すると新しいコピーが作成されます。

例: Python 文字列操作

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1])>

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s>

辞書

Python辞書 キー:値ペアの形式でデータを格納する、順序付けされていないデータのコレクションです。これは、時間計算量が O(1) である他の言語のハッシュ テーブルと似ています。 Python 辞書のインデックス付けはキーを使用して行われます。これらはハッシュ可能なタイプ、つまり文字列、数値、タプルなどのように決して変更できないオブジェクトです。中括弧 ({}) または辞書内包表記を使用して辞書を作成できます。

60 のうち 10 パーセント

例: Python 辞書の操作

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict)>

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25}>

マトリックス

行列は、各要素が厳密に同じサイズである 2D 配列です。マトリックスを作成するには、 NumPy パッケージ 。

例: Python NumPy 行列演算

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m)>

出力

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]]>

バイト配列

Python Bytearray は、0 <= x < 256 の範囲の可変の整数シーケンスを与えます。

例: Python バイト配列操作

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a)>

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e')>

リンクされたリスト

あ リンクされたリスト は線形データ構造であり、要素は連続したメモリ位置に格納されません。リンク リスト内の要素は、次の図に示すようにポインターを使用してリンクされます。

リンクされたリストは、リンクされたリストの最初のノードへのポインタによって表されます。最初のノードはヘッドと呼ばれます。リンクされたリストが空の場合、先頭の値は NULL になります。リスト内の各ノードは、少なくとも 2 つの部分で構成されます。

• データ
• 次のノードへのポインタ (または参照)

例: Python でのリンク リストの定義

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None>

3 つのノードを持つ単純なリンク リストを作成してみましょう。

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 |ヌル | | 3 |ヌル |  +----+------+ +----+------+ +----+------+ ''' 2 番目.次 = 3 番目; # 2 番目のノードを 3 番目のノード ''' にリンクします。これで、2 番目のノードの次が 3 番目を参照します。したがって、3 つのノードはすべてリンクされています。  llist.head 2 番目 3 番目 | | |  | | |  +-----+------+ +------+------+ +----+------+ | 1 | -------->| 2 | -------->| 3 |ヌル |  +----+------+ +----+------+ +----+------+ '''>>' 
リンクされたリストのトラバーサル
前のプログラムでは、3 つのノードを持つ単純なリンク リストを作成しました。作成されたリストを調べて、各ノードのデータを出力してみましょう。トラバーサルのために、指定されたリストを出力する汎用関数 printList() を作成しましょう。
Python3

1 2 3>

リンクリストに関するその他の記事

• リンクされたリストの挿入
• リンクリストの削除（指定されたキーの削除）
• リンクリストの削除（指定位置のキーを削除）
• リンクされたリストの長さを求める (反復的および再帰的)
• リンクされたリスト内の要素を検索 (反復的および再帰的)
• リンクリストの末尾から N 番目のノード
• リンクされたリストを反転する

あ スタック は、後入れ先出し (LIFO) または先入れ後出し (FILO) 方式で項目を格納する線形データ構造です。スタックでは、新しい要素が一方の端に追加され、要素はその端からのみ削除されます。挿入および削除操作は、プッシュおよびポップと呼ばれることがよくあります。

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty>

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: []>

スタックとして、 列 は、先入れ先出し (FIFO) 方式で項目を格納する線形データ構造です。キューを使用すると、最後に追加された項目が最初に削除されます。キューの良い例は、最初に来たコンシューマが最初に処理されるリソースのコンシューマのキューです。

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty>

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements []>

優先キュー は抽象データ構造であり、キュー内の各データ/値には特定の優先順位があります。たとえば、航空会社では、ビジネスクラスまたはファーストクラスというタイトルが付いた手荷物は、他の手荷物よりも早く到着します。 Priority Queue は、次のプロパティを持つキューの拡張です。

• 優先度の高い要素は、優先度の低い要素よりも前にデキューされます。
• 2 つの要素の優先度が同じ場合、それらはキュー内の順序に従って処理されます。

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] IndexError を除く項目を返します: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue) ただし、myQueue.isEmpty() ではありません: print(myQueue.delete())>>

12 1 14 7 14 12 7 1>

ヒープ

Pythonのheapqモジュール は、主に優先キューを表すために使用されるヒープ データ構造を提供します。このデータ構造の特性は、要素がポップされるたびに常に最小の要素 (最小ヒープ) を与えることです。要素がプッシュまたはポップされるたびに、ヒープ構造が維持されます。 heap[0] 要素も毎回最小の要素を返します。 O(log n) 回の最小要素の抽出と挿入をサポートします。

一般に、ヒープには次の 2 つのタイプがあります。

• 最大ヒープ: Max-Heap では、ルート ノードに存在するキーは、そのすべての子に存在するキーの中で最大である必要があります。同じプロパティが、そのバイナリ ツリー内のすべてのサブツリーに対して再帰的に true でなければなりません。
• 最小ヒープ: Min-Heap では、ルート ノードに存在するキーは、そのすべての子に存在するキーの中で最小である必要があります。同じプロパティが、そのバイナリ ツリー内のすべてのサブツリーに対して再帰的に true でなければなりません。

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li))>

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1>

ヒープに関するその他の記事

• バイナリ ヒープ
• 配列内の K 番目に大きい要素
• 未ソート配列内の K 番目の最小/最大要素
• ほぼソートされた配列をソートする
• K 番目に大きい合計の連続サブ配列
• 配列の数字から形成される 2 つの数値の最小合計

ツリーは、以下の図のような階層データ構造です。

 tree  ----  j <-- root  /   f k  /   a h z <-- leaves>

ツリーの最上位のノードはルートと呼ばれ、最下位のノードまたは子のないノードはリーフ ノードと呼ばれます。ノードの直下にあるノードはその子と呼ばれ、何かの直上にあるノードはその親と呼ばれます。

あ 二分木 は、要素がほぼ 2 つの子を持つことができるツリーです。バイナリ ツリー内の各要素は子を 2 つだけ持つことができるため、通常はそれらに left と right の子という名前を付けます。 Binary Tree ノードには次の部分が含まれます。

• データ
• 左の子へのポインタ
• 正しい子へのポインタ

例: ノードクラスの定義

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key>

次に、Python で 4 つのノードを持つツリーを作成しましょう。ツリー構造が以下のようだと仮定しましょう –

 tree  ----  1 <-- root  /   2 3   /  4>

例: ツリーへのデータの追加

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None'''>

ツリートラバーサル

木々を横切ることができる さまざまな方法で。以下は、ツリーを横断するために一般的に使用される方法です。以下のツリーを考えてみましょう –

 tree  ----  1 <-- root  /   2 3   /  4 5>

深さ優先トラバーサル:

• 順序 (左、ルート、右) : 4 2 5 1 3
• 予約注文 (ルート、左、右) : 1 2 4 5 3
• 事後順序 (左、右、ルート) : 4 5 2 3 1

アルゴリズムの順序(ツリー)

• 左側のサブツリーを走査します。つまり、Inorder(left-subtree) を呼び出します。
• ルートを訪問します。
• 右のサブツリーを走査します。つまり、Inorder(right-subtree) を呼び出します。

アルゴリズム事前注文(ツリー)

• ルートを訪問します。
• 左側のサブツリーを走査します。つまり、 Preorder(left-subtree) を呼び出します。
• 右のサブツリーをトラバースします。つまり、 Preorder(right-subtree) を呼び出します。

アルゴリズム 郵便注文(ツリー)

• 左側のサブツリーを走査します。つまり、Postorder(left-subtree) を呼び出します。
• 右のサブツリーをトラバースします。つまり、Postorder(right-subtree) を呼び出します。
• ルートを訪問します。

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root)>

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1>

時間計算量 – O(n)

幅優先またはレベル順のトラバーサル

レベル順序のトラバーサル ツリーの幅優先走査は、ツリーの幅優先の走査です。上記のツリーのレベル順序のトラバースは 1 2 3 4 5 です。

各ノードについて、まずそのノードが訪問され、次にその子ノードが FIFO キューに入れられます。以下は同じアルゴリズムです –

• 空のキューを作成します q
• temp_node = root /*ルートから開始*/
• temp_node が NULL でない間のループ
  • temp_node->data を出力します。
  • temp_node の子 (最初に左の子、次に右の子) を q にエンキューします。
  • qからノードをデキューします

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # キューの先頭を出力し、 # キューから削除します print (queue[0].data) node = queue.pop(0) # node.left が None でない場合、左側の子をキューに追加します: queue.append(node.left ) # node.right が None でない場合、右側の子をキューに追加します: queue.append(node.right) # 上記の関数をテストするドライバー プログラム root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print ('バイナリツリーのレベル順序トラバーサルは -') printLevelOrder(root)>>

Level Order Traversal of binary tree is - 1 2 3 4 5>

時間計算量: O(n)

バイナリ ツリーに関するその他の記事

• バイナリツリーへの挿入
• 二分木での削除
• 再帰なしの順序ツリー走査
• 再帰なし、スタックなしの順序ツリー走査!
• 指定された Inorder および Preorder トラバーサルから Postorder トラバーサルを印刷します
• プリオーダートラバーサルからBSTのポストオーダートラバーサルを見つける

二分探索木 は、次のプロパティを持つノードベースのバイナリ ツリー データ構造です。

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key)>

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r)>

20 30 40 50 60 70 80>

あ グラフ は、ノードとエッジで構成される非線形データ構造です。ノードは頂点と呼ばれることもあり、エッジはグラフ内の任意の 2 つのノードを接続する線または円弧です。より正式には、グラフは、頂点 (またはノード) の有限セットと、ノードのペアを接続するエッジのセットで構成されるグラフとして定義できます。

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0<=vtx<=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix())>

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # 上記のグラフ クラスへのドライバー プログラム if __name__ == '__main__' : V = 5graph = Graph(V)graph.add_edge(0, 1)graph.add_edge(0, 4)graph.add_edge(1, 2)graph.add_edge(1, 3)graph.add_edge(1, 4)グラフ.add_edge(2, 3) グラフ.add_edge(3, 4) グラフ.print_graph()>>

Adjacency list of vertex 0 head ->4 -> 1 頂点 1 頭部の隣接リスト -> 4 -> 3 -> 2 -> 0 頂点 2 頭部の隣接リスト -> 3 -> 1 頂点 3 頭部の隣接リスト -> 4 -> 2 -> 1 隣接頂点 4 のリスト -> 3 -> 1 -> 0>>

幅優先トラバーサル グラフの場合、ツリーの幅優先走査に似ています。ここでの唯一の注意点は、ツリーとは異なり、グラフにはサイクルが含まれる可能性があるため、同じノードに再び到達する可能性があることです。ノードを複数回処理することを避けるために、ブール値の訪問済み配列を使用します。簡単にするために、すべての頂点が開始頂点から到達可能であると仮定します。

たとえば、次のグラフでは、頂点 2 からトラバースを開始します。頂点 0 に到達したら、その頂点に隣接するすべての頂点を探します。 2 は 0 の隣接頂点でもあります。訪問した頂点をマークしないと、2 が再度処理され、非終了プロセスになります。次のグラフの幅優先トラバーサルは 2、0、3、1 です。

# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2)>

Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1>

時間計算量: O(V+E) ここで、V はグラフ内の頂点の数、E はグラフ内のエッジの数です。

深さ優先検索または DFS

深さ優先トラバーサル グラフの場合、ツリーの深さ優先探索に似ています。ここでの唯一の注意点は、ツリーとは異なり、グラフにはサイクルが含まれる可能性があり、ノードが 2 回アクセスされる可能性があることです。ノードを複数回処理しないようにするには、ブール値の訪問済み配列を使用します。

アルゴリズム：

• ノードのインデックスとアクセスした配列を取得する再帰関数を作成します。
• 現在のノードを訪問済みとしてマークし、ノードを出力します。
• すべての隣接ノードとマークされていないノードを走査し、隣接ノードのインデックスを使用して再帰関数を呼び出します。

# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2)>

Following is DFS from (starting from vertex 2) 2 0 1 3>

グラフに関するその他の記事

• セットとハッシュを使用したグラフ表現
• グラフ内の母頂点を見つける
• 反復深さ優先検索
• BFS を使用してツリー内の特定のレベルにあるノードの数をカウントします。
• 2 つの頂点間の可能なパスをすべて数えます

関数がそれ自体を直接的または間接的に呼び出すプロセスは再帰と呼ばれ、対応する関数は再帰と呼ばれます。 再帰関数 。再帰アルゴリズムを使用すると、特定の問題を非常に簡単に解決できます。このような問題の例としては、ハノイの塔 (TOH)、インオーダー/プレオーダー/ポストオーダー ツリー トラバーサル、グラフの DFS などがあります。

def fact(n):  # base case  if (n <= 1)   return 1  else   return n*fact(n-1)>

# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test)>

3 2 1 1 2 3>

• 再帰
• Python での再帰
• 再帰の練習問題 |セット1
• 再帰の練習問題 |セット2
• 再帰の練習問題 |セット3
• 再帰の練習問題 |セット4
• 再帰の練習問題 |セット5
• 再帰の練習問題 |セット6
• 再帰の練習問題 |セット 7

>>> 詳細

動的プログラミング

動的プログラミング これは主に単純な再帰に対する最適化です。同じ入力に対して繰り返し呼び出しを行う再帰的ソリューションが見つかった場合は、動的プログラミングを使用して最適化できます。考え方は、部分問題の結果を単純に保存して、後で必要になったときに再計算する必要がないようにすることです。この単純な最適化により、時間の複雑さが指数関数から多項式に軽減されます。たとえば、フィボナッチ数の単純な再帰的解法を作成すると、指数関数的な時間計算量が得られますが、部分問題の解を保存して最適化すると、時間計算量は線形に減少します。

表化とメモ化

サブ問題の値を再利用できるように、値を保存するには 2 つの異なる方法があります。ここでは、動的計画法 (DP) 問題を解く 2 つのパターンについて説明します。

• 集計: ボトムアップ
• メモ化: トップダウン

集計

名前自体が示唆しているように、下から始めて答えを上に積み上げていきます。状態遷移の観点から説明しましょう。

DP 問題の状態を、dp[0] を基本状態、dp[n] を目的の状態とする dp[x] として記述しましょう。したがって、目的の状態の値、つまり dp[n] を見つける必要があります。

基本状態、つまり dp[0] から遷移を開始し、状態遷移関係に従って目的の状態 dp[n] に到達する場合、遷移を開始したことが明らかであるため、これをボトムアップ アプローチと呼びます。一番下の基本状態から、一番上の望ましい状態に到達しました。

では、なぜ集計法と呼ぶのでしょうか？

これを知るために、まずボトムアップのアプローチを使用して数値の階乗を計算するコードを作成しましょう。もう一度、DP を解決するための一般的な手順として、最初に状態を定義します。この場合、状態を dp[x] として定義します。dp[x] は x の階乗を見つけることです。

さて、dp[x+1] = dp[x] * (x+1) であることは明らかです。

# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i>

メモ化

もう一度、状態遷移の観点から説明しましょう。ある状態の値を見つける必要がある場合、dp[n] とします。基本状態、つまり dp[0] から開始する代わりに、状態遷移後に目的の状態 dp[n] に到達できる状態から答えを求めます。関係がある場合、それはDPのトップダウン方式です。

ここでは、最上位の目的の状態から旅を開始し、最下位の基本状態に到達するまで、目的の状態に到達できる状態の値をカウントしてその答えを計算します。

C++の文字列分割

もう一度、階乗問題のコードをトップダウン形式で書いてみましょう

# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1))>

動的プログラミングに関するその他の記事

• 最適な部分構造特性
• 「重複する部分問題」プロパティ
• フィボナッチ数
• 合計が m で割り切れる部分集合
• 最大合計増加部分シーケンス
• 最長の共通部分文字列

>>> 詳細

検索アルゴリズム

線形探索

• arr[] の左端の要素から開始して、x を arr[] の各要素と 1 つずつ比較します。
• x が要素と一致する場合、インデックスを返します。
• x がどの要素とも一致しない場合は、-1 を返します。

# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result)>

Element is present at index 3>

上記のアルゴリズムの時間計算量は O(n) です。

詳細については、以下を参照してください。 線形探索 。

二分探索

検索間隔を半分に分割することを繰り返して、ソートされた配列を検索します。配列全体をカバーする間隔から始めます。検索キーの値が区間の中央の項目より小さい場合は、区間を下半分に絞ります。それ以外の場合は、上半分に絞ります。値が見つかるか、間隔が空になるまで繰り返しチェックします。

# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # 要素が中央自体に存在する場合 if arr[mid] == x: return Mid # 要素が Mid より小さい場合、それは # のみ存在可能左側の部分配列 elif arr[mid]> x: return binarySearch(arr, l, mid-1, x) # それ以外の場合、要素は右側の部分配列にのみ存在できます。それ以外の場合: return binarySearch(arr, Mid + 1, r, x) ) else: # 要素が配列に存在しません return -1 # ドライバー コード arr = [ 2, 3, 4, 10, 40 ] x = 10 # 関数呼び出しの結果 = binarySearch(arr, 0, len(arr)-1 , x) if result != -1: print ('要素はインデックス % d' % result) else: print ('要素は配列に存在しません')>>

Element is present at index 3>

上記のアルゴリズムの時間計算量は O(log(n)) です。

詳細については、以下を参照してください。 二分探索 。

ソートアルゴリズム

選択範囲の並べ替え

の 選択ソート アルゴリズムは、ソートされていない部分から最小の要素 (昇順を考慮) を繰り返し見つけて先頭に置くことによって配列をソートします。選択ソートを繰り返すたびに、ソートされていない部分配列から最小要素 (昇順を考慮) が選択され、ソートされた部分配列に移動されます。

選択ソートのフローチャート:

# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # 見つかった最小要素を # 最初の要素と交換します A[i], A[min_idx] = A[min_idx], A[i] # 上記をテストするドライバー コード print ('ソートされた配列') for i in range(len(A)): print('%d' %A[i]),>

Sorted array 11 12 22 25 64>

時間計算量: の上²) ネストされたループが 2 つあるためです。

補助スペース: ○(1)

バブルソート

バブルソート は、順序が間違っている場合に隣接する要素を繰り返し交換することで機能する、最も単純な並べ替えアルゴリズムです。

イラスト：

# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # 上記をテストするドライバーコード arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('ソートされた配列は:') for i in range(len(arr)): print ('%d' %arr[i]),>

Sorted array is: 11 12 22 25 34 64 90>

時間計算量: の上²)

挿入ソート

サイズ n の配列を昇順に並べ替えるには、次を使用します。 挿入ソート :

• 配列に対して arr[1] から arr[n] までを繰り返します。
• 現在の要素 (キー) をその前の要素と比較します。
• キー要素がその前の要素より小さい場合は、前の要素と比較します。大きい要素を 1 つ上の位置に移動して、交換された要素用のスペースを確保します。

図：

# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 とキー< arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i])>

 5 6 11 12 13>

時間計算量: の上²))

マージソート

クイックソートと同様に、 マージソート 分割統治アルゴリズムです。入力配列を 2 つの半分に分割し、その 2 つの半分に対して自分自身を呼び出し、その後、ソートされた 2 つの半分をマージします。 merge() 関数は、2 つの半分を結合するために使用されます。 merge(arr, l, m, r) は、arr[l..m] と arr[m+1..r] がソートされていることを前提として、ソートされた 2 つの部分配列を 1 つにマージする重要なプロセスです。

MergeSort(arr[], l, r) If r>l 1. 配列を 2 つの半分に分割するための中点を見つけます: middle m = l+ (r-l)/2 2. 前半で mergeSort を呼び出します: Call mergeSort(arr, l, m) 3. 後半で mergeSort を呼び出します: Call mergeSort(arr, m+1, r) 4. ステップ 2 と 3 でソートした 2 つの半分をマージします。 merge(arr, l, m, r) を呼び出します。 
  
Python3 
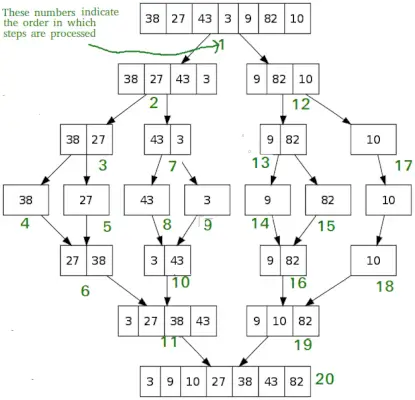
# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # 配列の中央を見つける Mid = len(arr)//2 # 配列要素を分割 L = arr[:mid] # 2 つの半分に R = arr[mid:] # 前半を並べ替える mergeSort(L) # 後半のソート mergeSort(R) i = j = k = 0 # i 中に一時配列 L[] と R[] にデータをコピー< len(L) and j < len(R): if L[i] < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i < len(L): arr[k] = L[i] i += 1 k += 1 while j < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr)>
   
  出力      時間計算量:    O(n(logn))
 
クイックソート
マージソートと同様に、  クイックソート  分割統治アルゴリズムです。要素をピボットとして選択し、選択したピボットを中心に指定された配列を分割します。 QuickSort には、さまざまな方法でピボットを選択するさまざまなバージョンが存在します。
 
常に最初の要素をピボットとして選択します。
 
常に最後の要素をピボットとして選択します (以下で実装)
ランダムな要素をピボットとして選択します。
中央値をピボットとして選択します。
QuickSort の主要なプロセスは、partition() です。パーティションのターゲットは、配列と配列の要素 x をピボットとして指定し、並べ替えられた配列の正しい位置に x を配置し、すべての小さな要素 (x より小さい) を x の前に配置し、より大きな要素 (x より大きい) をすべて x の後に配置します。バツ。これらすべては線形時間内に実行される必要があります。
 
/* low -->開始インデックス、high --> 終了インデックス */quickSort(arr[], low, high) { if (low { /* pi はパーティション化インデックス、arr[pi] は正しい場所にあります */ pi = Partition(arr, low, high); easySort(arr, low, pi - 1); // pi 前 QuickSort(arr, pi + 1, high) // pi 後 } }>'
 
 
    パーティションアルゴリズム    
 
パーティションを作成するには、次のようなさまざまな方法があります。  疑似コード  CLRS本に記載されている方法を採用しています。ロジックは単純で、一番左の要素から開始して、より小さい (または等しい) 要素のインデックスを i として追跡します。トラバース中に、より小さい要素が見つかった場合は、現在の要素を arr[i] と交換します。それ以外の場合は、現在の要素を無視します。
  
# Python3 implementation of QuickSort # This Function handles sorting part of quick sort # start and end points to first and last element of # an array respectively def partition(start, end, array): # Initializing pivot's index to start pivot_index = start pivot = array[pivot_index] # This loop runs till start pointer crosses # end pointer, and when it does we swap the # pivot with element on end pointer while start < end: # Increment the start pointer till it finds an # element greater than pivot while start < len(array) and array[start] <= pivot: start += 1 # Decrement the end pointer till it finds an # element less than pivot while array[end]>pivot: end -= 1 # start と end が交差していない場合、 # start と end の数値を入れ替える if(start< end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}')>
   
  出力  
Sorted array: [1, 5, 7, 8, 9, 10]>
 
    時間計算量:    O(n(logn))
 
シェルソート
 シェルソート これは主に挿入ソートのバリエーションです。挿入ソートでは、要素を 1 つだけ前に移動します。要素をはるか前方に移動する必要がある場合、多くの動きが必要になります。 shellSort のアイデアは、遠い項目の交換を可能にすることです。 shellSort では、h の値が大きい場合に配列を h ソートします。 h の値が 1 になるまで減らし続けます。配列は、すべての h のすべてのサブリストが存在する場合に h ソートされていると言われます。番目要素がソートされます。
Python3 
# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = ギャップ # 配列を左から右にチェックします # j の可能な最後のインデックスまで、j の間< len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # ここで、i 番目のインデックスから左に戻ります # 値を交換します正しい順序ではありません。 k = i のとき、k - ギャップ> -1: arr[k - ギャップ]> arr[k] の場合: arr[k-gap],arr[k] = arr[k],arr[k-gap] k -= 1 ギャップ //= 2 # コードをチェックするドライバー arr2 = [12, 34, 54, 2, 3] print('入力配列:',arr2) shellSort(arr2) print('ソートされた配列', arr2)>>'  
  出力      時間計算量:    の上2）。