線は一次元の幾何学的形状であり、その両側は無限に広がります。ジオメトリには、形状、方向、交差に基づいてさまざまなタイプの線があります。さまざまな点について学びましょう ジオメトリ内の線の種類 とその応用について詳しく説明します。
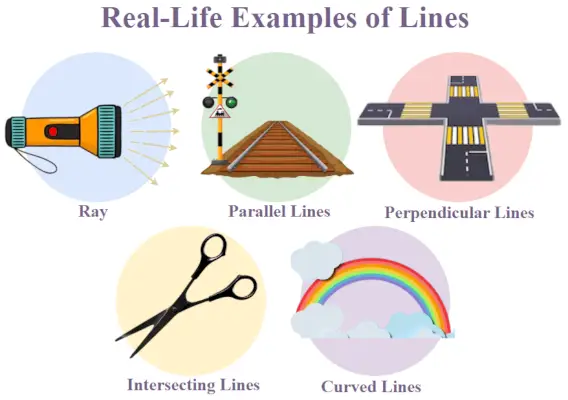
目次
ラインとは
ライン 両方向に無限に伸びる無限の点の組み合わせです。これは、幅のない長さを持つ 1 次元の形状として定義されます。
通常、両端に矢印が付いた直線で表されます。矢印は無限の延長を表します。
Javaで更新する方法
レイとは何ですか
一方向に無限に伸び、もう一方の端点が固定された直線を「直線」といいます。 光線 。光線は片側から無限に伸ばすことができるので。定義された長さはありません。
たとえば、A が端点、B が光線の方向の点である場合、次のように表すことができます。 光線AB または単に 光線A 。
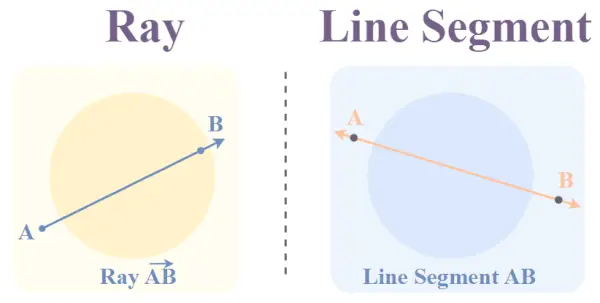
光線と線分の図
線分とは
2 つの端点を持つ線分を線分と呼びます。言い換えれば、線分は線の小数部です。
これは通常、線上にある任意の 2 つの点によって表され、各点には何らかのアルファベットの名前が付いています。たとえば、線分の 2 つの端点が A と B である場合、その線分は AB と同じように書くことができます。
線の種類
ジオメトリにはさまざまな種類の線があり、さまざまなプロパティや特徴があります。
- 構造に基づく線の種類
- 直線
- 曲線
- ジグザグ線
- 破線または破線
- 向きに基づく線の種類
- 水平線
- 縦線
- 斜線
- 交差点に基づく線の種類
- 交差する線
- 二等分線
- 垂直線
- 平行線
- 横線
形状に基づく線の種類
形状または方向の変化に基づいて、線を次のように分類できます。
- 直線
- 曲線
- ジグザグ線
- 破線または破線
それらについて詳しく説明しましょう。
直線
直線とは、無限に伸びても直線経路から逸脱しない線のことです。これらの線は方向が同じで曲率が全くないのが特徴です。
直線は両方向に無限に延長できます。線は同じ一定の傾き (正の X 軸からの角度) を持ちます。
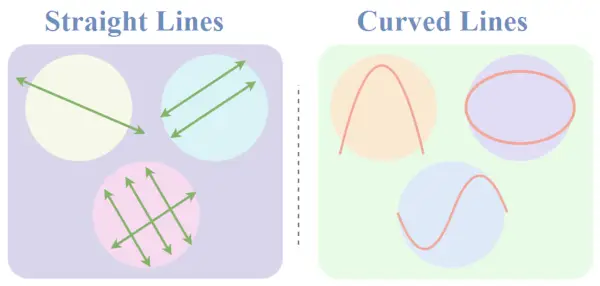
直線と曲線のイラスト
曲線
曲線は、方向が徐々に変化する線です。それらの傾きは、異なる値の間で徐々に変化します。直線とは異なり、直線的なパスをたどることはありません。
曲線を閉じると、円や楕円などのさまざまな幾何学的オブジェクトを形成でき、閉じていない場合は、らせん、円弧、放物線などの曲率を作成できます。
ジグザグライン
ジグザグ線は、傾きが突然変化する、鋭く尖った線分の集まりです。これらの線は、正と負の傾きが交互に並ぶ一連の接続された線分で構成されています。
これらの線は、一連の Z または N 形状に似ており、ギザギザの線を形成します。ジグザグ線の主な使用例はアートやグラフィック デザインで、これらの線は突然の急速な変化やダイナミックな動きを表現するために使用されます。
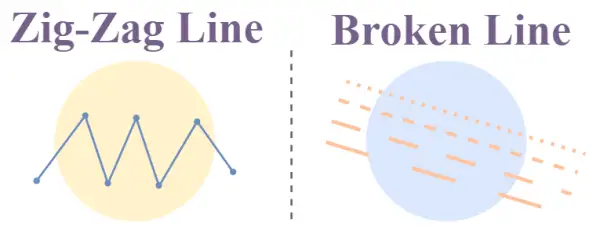
ジグザグと破線のイラスト
破線
破線は、直線上に配置された多数の小さな線分の集合であり、各線分の長さは使用例に応じて異なります。
これらの線分は破線のように見えるため、破線とも呼ばれます。
向きに基づく線の種類
- 水平線
- 縦線
- 斜線
それらについて詳しく説明しましょう。
向きに基づく線の種類
水平線
水平線は、水平軸、つまり x 軸または地面に平行な線です。言い換えれば、左から右、またはその逆に向かう線は水平線と呼ばれます。
春のjpa
代数学では、方程式 y = 定数を使用して水平線を表すことができます。
垂直線
垂直線は水平線の反対であり、垂直軸、つまり y 軸に平行です。つまり、地面に対して垂直な線を垂直線と呼びます。
これらの線は上下方向に伸びており、現実世界ではこれらの線が電柱、多層階の建物、構造物を支える柱などとして見ることができます。
斜線
斜めの線は、水平方向と垂直方向の間にある傾きにあるため、水平方向にも垂直方向にも行かない線です。
斜線とも呼ばれます。
交差点に基づく線の種類
- 交差する線
- 二等分線
- 垂直線
- 平行線
- 横線
それらについて詳しく説明しましょう。
交差する線
交差線とは、共通の点で交わるか交差する 2 本以上の線です。これらの線が交わる点を 交差点。
代数学では、この交点は 2 本の直線によって形成される方程式系の解となります。
Javaで現在の日付を取得する
交差線と二分線の図
二等分線
二等分線とは、線分を 2 つの等しい部分に分割する線です。そのオブジェクトは、角度、三角形、任意の多角形、または線分にすることができます。オブジェクトの中点を通過します。
二等分線は、角度または線分を均等に分割するために幾何学でよく使用されます。
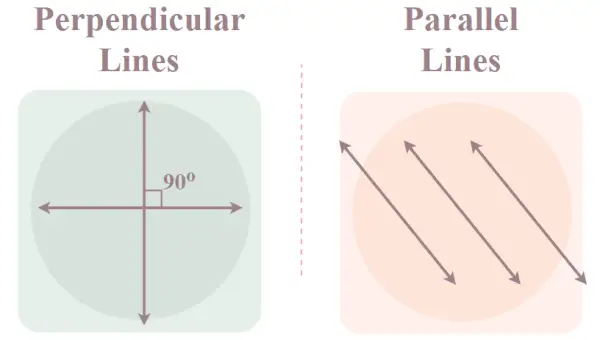
垂直線
垂直線とは、互いに直角をなす交差する線のことです。このような垂直線のペアの 1 つが、交差する場合は垂直線と水平線になります。また、垂線の傾きには相関関係があり、垂線の傾きの積は常に-1となります。たとえば、1 本の線の傾きが 2 の場合、垂線の傾きは -1/2 になります。
垂直線と平行線の表現
続きを読む:
平行線
平行線は交差線の逆であり、どれだけ延長しても決して交差しません。すべての平行線の傾きは同じですが、y 切片が異なります。
代数学では、定数部分を除いて、すべての平行線は同様の方程式を持ちます。たとえば、直線 y = 2x + 1 と y = 2x – 3 は平行です。
続きを読む:
- 平行線
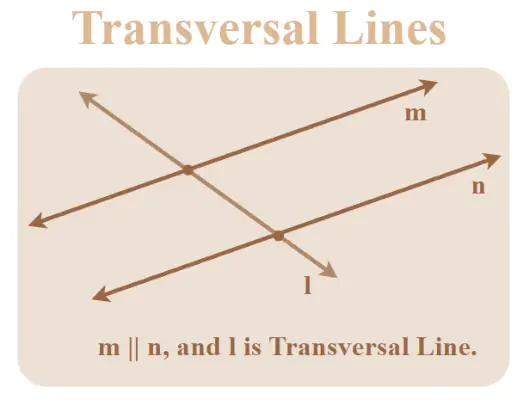
横線
横線は、他の 2 本以上の線と交差する線です。
2 本の線の場合、横線は 8 つの角度を形成し、平行線の場合、これら 8 つの角度はさまざまな性質と関係を示します。これらの角度の一部は、対応する角度、交互の内角、交互の外角、および連続する内角です。
横線のイラスト
特殊な種類の線
ジオメトリには、次のようなさまざまな特殊なタイプの線があります。
- 接線
- 割線
- スキューライン
- 対称線
それらについて詳しく説明しましょう。
接線
接線は、曲線または幾何学的オブジェクトに一点でのみ接触し、その後は二度と交差しない線として定義されます。
- 接触点では、接線と曲線は同じ傾きになります。つまり、
y = f(x) の場合、dy/dx が指定された曲線です。
- 2 次元の場合、任意の点における任意の曲線の接線は、傾きと同じ瞬間的な変化率を表します。
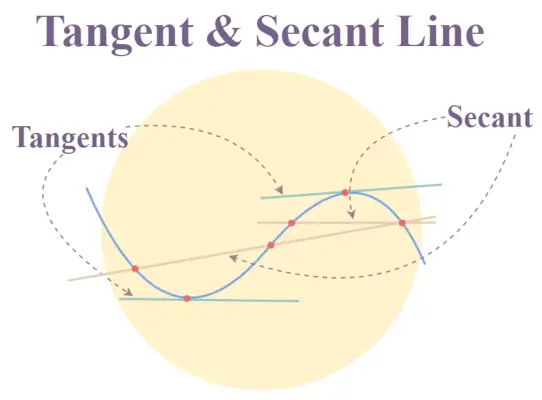
接線と割線の図
ローマ数字 1 ~ 100
割線
一方、割線は接線とは異なり、これらの線は 2 つ以上の別個の点で曲線または円などの幾何学的オブジェクトと交差します。円に対する割線には接割定理と交互割線定理と呼ばれるいくつかの性質があります。
スキューライン
3 次元空間では、スキュー ラインは、互いに交差も平行もしない線のペアです。これらは 2 次元に対しては定義されていません。

対称線
対称線は、形状を 2 つの合同な半分に分割する線です。 2 つの半分は互いの鏡像です。このことから、対称線はミラーラインとも呼ばれます。
この概念は、多角形、文字、オブジェクトなどのさまざまな幾何学的形状に適用されます。

pd.merge
続きを読む:
- 線と角度
- 角度の種類
- 点、線、面
回線の種類に関するよくある質問
ラインとは何ですか?
線とは、両方向に無限に伸びる直線のパスです。端点がなく、多くの場合、両端に矢印が付いた直線を使用して表されます。線は、両方向に無限に伸びる点の集合と考えることができます。
レイを定義します。
光線は、終点と呼ばれる特定の始点から一方向に無限に伸びる直線です。反対方向にはエンドポイントが定義されておらず、無限に継続します。
線分を定義します。
線分は、空間内の 2 点間の直線パスです。これは、エンドポイントとそれらの間にあるすべてのポイントで構成されます。線とは異なり、線分には定義された長さがあり、測定できます。
線分と線分の違いは何ですか?
線は無限に長く端点がありませんが、線分には 2 つの異なる端点があります。
幾何学には何種類の線がありますか?
さまざまなパラメータに基づいたさまざまなタイプのラインは、
- 直線
- 曲線
- ジグザグ線
- 破線または破線
- 水平線
- 縦線
- 斜線
- 交差する線
- 二等分線
- 垂直線
- 平行線
- 横線
垂直線とは何ですか?
垂直線は、別の線または面と 90 度の角度を形成する線です。 2 本の線が交差し、形成される角度がすべて 90 度である場合、それらは互いに垂直であると言われます。
平行線とは何ですか?
平行線とは、同じ平面上にあり、どれだけ伸ばしても決して交わらない線のことです。それらは同じ傾きを持ち、常に同じ距離を維持します。
平行線は交わるのか?
いいえ、平行線は決して交わることはありません。たとえそれらの線を無限の距離まで延長したとしても、それらは決して交わることはありません。
交差線とは何ですか?
交差線とは、交点と呼ばれる特定の点で別の線と交差または交わる線です。 2 本の線が交差する場合、それらは共通点を共有します。
横線とは何ですか?
横線は、異なる点で 2 つ以上の他の線と交差する線です。交差する線によって、対応する角度、交互の内角、交互の外角など、さまざまな角度を形成します。
スキューラインとは何ですか?
斜線は、同じ平面上になく、平行でも交差でもない線です。これらは、空間内を移動しながら相互間に一定の距離を維持する非共面線です。
接線とは何ですか?
接線は、曲線またはサーフェスに 1 点で接し、それ以上交差しない線です。これは、その点における曲線の瞬間的な方向を表します。
同時実行ラインとは何ですか?
平行線は、単一点で交差する平面内の 3 本以上の線です。この共通の交差点は同時実行点として知られています。
