単位円は半径 1 の円です。単位円の中心は軸上の原点(0,0)にあります。の 周 単位円の面積は π 単位であるのに対し、単位円の面積は 2π 単位です2。 Circle のすべてのプロパティが含まれています。単位円には方程式 x があります2+と2= 1. この単位円は、さまざまな三角法の概念を定義するのに役立ちます。
単位円
単位円は S として表されることがよくあります。1高次元への一般化は単位球です。以下で、単位円、公式、解決例について詳しく理解しましょう。
単位円とは何ですか?
単位円は、半径が 1 単位の円です。デカルト平面を使用して単位円を描画します。単位円は 2 つの変数を含む 2 次の多項式です。単位円は三角法や代数学でさまざまな応用があり、主に sin x、cos x、tan x などのさまざまな三角比の値を求めるために使用されます。
単位円の定義
数学では、単位円を、円の中心から 1 単位の距離にある固定点の軌跡として定義します。単位円の半径は 1 単位であるため、単位円と呼ばれます。
単位円の方程式
中心 (h, k) と半径「r」を持つ円の方程式は次のとおりであることがわかっています。
(x – h) 2 + (y – k) 2 = r 2
単位円の場合、r が 1 単位であることがわかっているため、単位円の方程式は次のようになります。
(x – h) 2 + (y – k) 2 = 1
単位円の公式
単位円の中心が原点、つまり (h, k) = (0, 0) の場合、単位円の方程式は次のようになります。
バツ 2 +と 2 = 1
以下に追加した画像では、単位円が中心座標 h、k で表されており、円が原点にあるとき、h と k の値は 0 で、半径 AP は 1 単位に等しくなります。
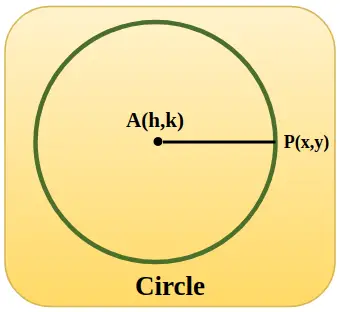
単位円を使用した三角関数
ピタゴラスの定理を単位円に適用すると、三角関数を理解するのに適しています。このために、直角三角形がデカルト座標平面の単位円の内側に配置されると考えます。注目すると、この円の半径は直角三角形の斜辺を示します。
円の半径はベクトルを形成します。これにより、正の x 軸と角度、たとえば θ が形成されます。直角三角形の底辺の長さを x 、高度の長さを y とします。また、動径ベクトルの端点の座標はそれぞれ(x,y)となります。
直角三角形はそれぞれ辺 1、x、y を保持します。三角比は次のように計算できるようになりました。
Java参照型
sinθ = 高度/斜辺 = y/1
cosθ = 底辺/斜辺 = x/1
今、
- sinθ = y
- cosθ = x
- Tanθ = sinθ /cosθ = y/x
θ の値を代入すると、すべての三角関数の主値が得られます。同様に、異なる値の三角関数の値も求められます。
Sin Cos と Tan を含む単位円
座標 (x, y) を持つ単位円上の任意の点は、三角関数の恒等式を使用して (cosθ, sinθ) として表されます。半径のコーナーの座標は、特定の θ 値と半径線の θ 値のコサインとサインを表します。 cos θ = x、sin θ = y です。円には 4 つの部分があり、それぞれ 1 つの象限内にあり、90°、180°、270°、360° の角度を形成します。半径の値はそれぞれ -1 ~ 1 の間にあります。また、sin θ と cos θ の値はそれぞれ 1 と -1 の間にあります。
単位円と三角恒等式
コタンジェント、セカント、コセカントの単位円三角恒等式は、sin、cos、tan の恒等式を使用して計算できます。最終的に、それぞれ辺 1、x、y を持つ直角三角形が得られます。単位円恒等式の計算は次のように表すことができます。
- sinθ = y/1
- cosθ = x/1
- タンθ = y/x
- 秒 θ = 1/x
- cosec θ = 1/y
- コットθ = x/y
単位円グラフ
単位円グラフは、さまざまな角度の三角関数のサインとコサインの値を含むグラフです。同じ単位円グラフを以下に追加します。
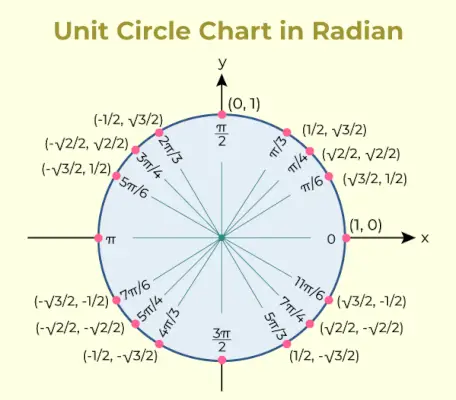
単位円表
単位円テーブルで使用される三角比は、一般的な角度に対応する単位円上の点の座標をリストするために使用されます。
| 角度 | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| それなし | 0 | 1/2 Java文字列 | 1/√(2) | √3/2 | 1 |
| コス | 1 | √3/2 | 1/√(2) | 1/2 | 0 |
| それで | 0 | 1/√(3) math.random Java | 1 | √(3) | 定義されていません |
| csc | 定義されていません | 2 | √(2) | 23) | 1 |
| 秒 | 1 | 23) | √(2) | 2 | 定義されていません |
| ベビーベッド | 定義されていません | √(3) | 1 | 1/√(3) | 0 |
ユニットサークルのピタゴラス恒等式
3 つのピタゴラス恒等式があり、それらはすべて、3 つのピタゴラス恒等式の単位円の概念を使用して簡単に証明されます。
- それなし2θ+cos2θ = 1
- 1 + それで2θ = 秒2私
- 1 + ベビーベッド2θ = コ秒2私
単位円複素平面
複素数 と複素平面は、単位円の概念を使用して簡単に説明できます。複素形式の単位円の方程式は次のとおりです。
|z| = 1
typescript の日付型または
バツ 2 +と 2 = 1
オイラーの形式では、複素数は次のように表されます。
z = e それ = コスト + i(sin t)
続きを読む
単位円に関する解決例
Q1: 点 Q が単位円上にあることを証明してください、Q = [1/√(6), √4/√6]
解決:
考えると、
- Q = [1/√(6)、√4/√6]
x = 1/√(6)、y = √4/√6
単位円の方程式は、
バツ2+と2= 1
左=(1/√(6))2+ (√4/√6)2
左 = 1/6 + 4/6 = 5/6 ≠ 1
左≠右
したがって、点 Q[1/√(6), √4/√6] は単位円上にありません。
Q2: 30 を計算してください ○ 単位円の sin 値と cos 値を使用します。
解決:
sin 値と cos 値を使用した Tan 30°、
Tan 30° = (sin 30°)/(cos 30°)
- 30°なし = 1/2
- cos 30° = √(3)/2
タン 30° = 1/2/√(3)/2
Tan 30° = 1/√(3)
Q3: 点 P [1/2, √(3)/2] が単位円上にあるかどうかを検証します。
解決:
考えると、
P = [1/2、√(3)/2]
- x = 1/2
- y = √(3)/2
単位円の方程式は、
- バツ2+と2= 1
左
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= 右軸
単位円に関する練習問題
Q1.点 A (1/2、3/2) が単位円上にあるかどうかを確認します。
Q2.点 A (2, 1/2) が単位円上にあるかどうかを確認します。
Q3. cos 240°の値を求める
Q4. Tan 320°の値を求める
Q5. sin 160°の値を求める
ユニットサークル – よくある質問
単位円とは何ですか?
単位円は、固定点から 1 単位離れた点の位置として定義されます。中心は (0,0) にあり、半径の値は 1 です。
ポイントがユニット サークレット上にあるかどうかを確認するにはどうすればよいですか?
2D 平面内にある (x, y) の形式の点はすべて、単位円方程式 x に入れられます。2+と2= 1 は円上にあるかどうかを確認します。
文字列が長すぎる
単位円の公式は何ですか?
単位円公式は、単位円を代数的に表すために使用される公式です。単位円の公式は次のように与えられます。
バツ 2 +と 2 = 1
なぜ単位円と呼ばれるのですか?
単位円は半径が 1 単位であるため、単位円と呼ばれます。
