円は、円の中心からすべて同じ距離にある点で構成されます。閉じた幾何学的形状は円です。日常生活では、車輪、ピザ、丸い地面などの形をした円が見られます。
円の一部
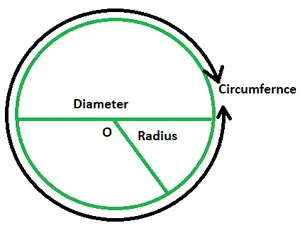
重要な用語:
- 半径: の 円の半径 は、その中心とエッジ上の任意の点の間の距離です。一般的にはrと表記されます。円には無限の半径があります。
- 直径: 中心を通り、円上に端がある線です。これは D で示され、円の半径の 2 倍の値です。
- 周: 円の境界線の範囲は円周と等しくなります。これは、円の周長がその円周に等しいことを意味します。円の円周は、その周囲をきれいに包み込む糸の長さに等しくなります。それは 2πr として与えられます。
円の面積とは何ですか?
円の面積は、円のエッジによって囲まれる空間の量に関係します。円で満たされた領域は、円の周囲内の領域です。円内に含まれる正方形ユニットの総量としても知られています。
チェック: 円の直径
円の面積の公式
円の表面積は次の式で求められます。
A = πr 2
ここで、r は指定された円の半径です。
または
A = C 2 /4p
ここで、C は指定された円の円周です。
円の面積公式を使用した例
質問 1. 半径 8 m の円の面積を求めます。
解決:
与えられた場合: r = 8 m
円の面積 = πr なので2
A = π(8)2
= 64p
dhlとはどういう意味ですか= 200.96メートル 2
問題 2. 円周 12 cm の円の面積を求めてください。
解決:
与えられた場合: C = 12 cm
したがって、A = C2/4p
= 122/4p
= 11.46cm 2
問題 3. 直径 12 cm の円の面積を求めます。
解決:
与えられた場合: D = 12 cm
または、半径 = r = 12/2 = 6 cm
A = πr なので2
= π(6)2
= 113.04cm 2
質問 4. 半径 9 cm の円の面積を求めます。
解決:
与えられた場合: r = 9 m
円の面積 = πr なので2
A = π(9)2
= 81p
= 254.34cm 2
問題 5. 直径 10 cm の円の面積を求めてください。
解決:
与えられた場合: D = 10 cm
または、半径 = r = 10/2 = 5 cm
A = πr なので2
= π(5)2
モデルの例= 78.5cm 2
以下もチェックしてください:
- 円の面積計算機
- 円計算機の平方フィート
- 円の半径計算機
- 円の直径計算機
- 円周計算機
- 円周から直径への計算
